题目内容
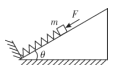
【题目】如图所示，沿倾角为θ的斜面放置的劲度系數为k轻弹簧，一端固定在挡板上，另一端与质量为m的小物块接触(但无挤压)。先用沿斜面向下的力F缓慢推动物块，当弹簧的压缩量为x时，撤去F，物块沿斜面向上运动，运动的最大距离为3x。已知物块与斜面间的动摩擦因数为μ，重力加速度为g.则
A. 撤去F时.弹簧的弹性势能为2mgx(sinθ+μcosθ)
B. 撤去F时，物块加速度的值为
C. 从撤去F到沿斜面上升至最高点的过程中，物块做匀变速运动的时间为
D. 从撤去F到沿斜面向上速度最大的过程中，物块克服重力做的功为
【答案】BD
【解析】由题知，物体运动的最大距离为3x，可知物体的动能变化量为0，根据动能定理得：
，解得：
，即撤去F时弹性势能为
，故A错误；撤去F时根据牛顿第二定律得：
，解得：
，故B正确；当物块向上运动x远时，弹簧回到原长，设此时物块的速度为v，由动能定理得：
，解得：
，再经过2x速度为0，则有：
，解得：
，故C错误；当物块的速度最大时，物块的合外力为0，即
，解得：
，故物块克服重力做的功为
，故D正确；故选BD.
练习册系列答案
相关题目
