题目内容
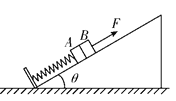
【题目】如图所示，平行于光滑固定斜面的轻弹簧劲度系数为k，一端固定在倾角为θ的斜面底端，另一端与物块A连接，质量为m物块B在斜面上紧靠着物块A但不粘连，初始时两物块均静止。现用平行于斜面向上的力F拉动物块B，使B做加速度为ɑ的匀加速运动，已知前一段时间内，F是变力，之后F是恒力，已知重力加速度为g，则
A. 若A的质量为m，则A达到最大速度时的位移为
B. 若A的质量忽略不计，则A的最大位移为
C. 无论是否计A的质量，A、B都是在斜面上同一位置处分离
D. 无论是否计A的质量，A、B与弹簧组成的系统机械能守恒
【答案】AB
【解析】由图知，A的加速度为零，速度最大，根据牛顿第二定律和胡克定律得：mgsinθ=kx，
得：x=
，故A正确；若A的质量不计，则两物体在弹簧原长位置分离，对AB整体，不受拉力时弹力：F弹=mgsinθ，根据胡克定律，压缩量：x=
，故A的最大位移为：xm=
，故B正确； 物体AB刚分离时，AB间弹力为零，对物体A，有：F弹-mgsinθ=ma，故取不同的质量，弹簧弹力不同，分离位置不同，故C错误；对AB组成的系统，有拉力和弹簧弹力做功，故机械能不守恒，故D错误；故选AB.
练习册系列答案
相关题目
