题目内容
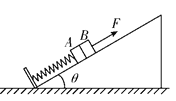
【题目】如图所示，半径为R的光滑圆弧轨道ABC竖直放置，A与圆心O等高，B为轨道的最低点，该圆弧轨道与一粗糙直轨道CD相切于C，OC与OB的夹角为53°。一质量为m的小滑块从P点由静止开始下滑，PC间距离为R，滑块在CD上滑动摩擦阻力为重力的0.3倍。（sin53°= 0.8，cos53°= 0.6）求：
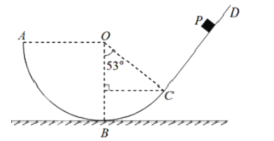
(1) 滑块从P点滑至B点过程中，重力势能减少多少？
(2) 滑块第一次经过B点时所受支持力的大小；
(3) 为保证滑块不从A处滑出，PC之间的最大距离是多少？
【答案】（1）h=1.2R（2）F=2.8mg（3）L=1.2R
【解析】（1）如图所示，PC间的竖直高度
CB间的竖直高度 
所以PB间高度差 
①
所以滑块从P滑到B减少的重力势能为 
②
（2）对B点，由牛顿第二定律知 
③
从P到B，由动能定理： 
④
联立解得： 
⑤
（3）设PC之间的最大距离为L时，滑块第一次到达A时速度为零，则对整个过程应用动能定理： 
⑥
代入数值解得： 
⑦
练习册系列答案
互动课堂系列答案
激活思维智能训练课时导学练系列答案
相关题目
