Question

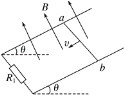
【题目】如图所示，两条电阻不计的平行导轨与水平面成θ角，导轨的一端连接定值电阻 R1，匀强磁场垂直导轨平面向上。一根质量为 m、电阻为 R2 的导体棒 ab，垂直导轨放置且两端始终与导轨接触良好，导体棒与导轨之间的动摩擦因数为μ，且 R2=nR1。如果导体棒以速度v 匀速下滑，导体棒此时受到的安培力大小为F，则以下判断正确的是（ ）

A.电阻 R1 消耗的电功率为

B.重力做功的功率为 mgvsinθ

C.运动过程中减少的机械能全部转化为电能

D.R2 上消耗的功率为

Answer 1

【答案】BD

【解析】

A． 导体棒以速度v匀速下滑时，由E=BLv、，F=BIL，推导出

电阻R1消耗的热功率为

又R2=nR1以上各式联立得解得：

故A错误；

B． 根据瞬时功率表达式：P=Fvcosα（其中α为F与v之间的夹角）可知，重力做功的功率为：

故B正确；

C． 根据能量守恒定律可知：运动过程中减少的机械能转化为电能和摩擦产生的热量，故C错误；

D． 电阻R2消耗的热功率为

结合以上分析可知

故D正确。

故选BD。