题目内容
如下左图所示,真空中有两水平放置的平行金属板C、D,上面分别开有正对的小孔O1和O2,金属板C、D接在正弦交流电源上,两板间的电压uCD随时间t变化的图线如下右图所示。t=0时刻开始,从D板小孔O1处连续不断飘入质量为m=3.2×10-25kg,电荷量为q=1.6×10-19C的带正电的粒子(设飘入速度很小,可视为零)。在C板外侧有以MN为上边界CM为左边界的匀强磁场,MN与C金属板平行,相距d=10cm,O2C的长度L=10cm,匀强磁场磁感应强度的大小为B=0.10T,方向如图所示,粒子的重力及粒子间相互作用力忽略不计。平行金属板C、D之间的距离足够小,粒子在两板间的运动时间可忽略不计。求:
⑴带电粒子经小孔O2进入磁场后,能飞出磁场边界MN的最小速度为多大?
⑵从0到0.04s末时间内哪些时间段飘入小孔O1的粒子能穿过电场并飞出磁场边界MN?
⑶磁场边界MN有粒子射出的长度范围有多长。(计算结果保留三位有效数字)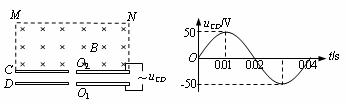
(1)设粒子飞出磁场边界MN的最小速度为v0,粒子在磁场中做匀速圆周运动,根据洛伦兹力提供向心力知:
qv0B=mv02/R0 (2分)
粒子恰好飞出磁场,则有:R0=d (2分)
所以最小速度 v0=qBd/m=5×103m/s (2分)
(2)由于C、D两板间距离足够小,带电粒子在电场中运动时间可忽略不计,故在粒子通过电场过程中,两极板间电压可视为不变,设恰能飞出磁场边界MN的粒子在电场中运动时CD板对应的电压为U0,则根据动能定理知:
qU0=mv02/2 (2分)
得:U0=mv02/2q=25V (2分)
根据图像可知:UCD=50sin50πt,25V(或-25V)电压对应的时间分别为: 7/300s和11/300s,所以粒子在0到0.04s内飞出磁场边界的时间为7/300s—11/300s (2分)
(3)设粒子在磁场中运动的最大速度为vm,对应的运动半径为Rm,则有:
qUm=mvm2/2 (1分) qvmB=mvm2/Rm (1分)
粒子飞出磁场边界时相对小孔向左偏移的最小距离为:
x=Rm-(Rm2-d2)1/2=0.1×(21/2-1)m≈0.0414m (2分)
磁场边界MN有粒子射出的长度范围为:△x=d-x=0.0586m (2分)

 通城学典默写能手系列答案
通城学典默写能手系列答案
 如图所示,真空中有两个电量相同的正电荷A、B相距L放置,在AB连线的中垂线上有a、b、c三点,b点在AB连线的中点上,a较c离b近一些,现若将A、B两电荷同时向两边扩大相同距离,设无穷远处电势为零,则有( )
如图所示,真空中有两个电量相同的正电荷A、B相距L放置,在AB连线的中垂线上有a、b、c三点,b点在AB连线的中点上,a较c离b近一些,现若将A、B两电荷同时向两边扩大相同距离,设无穷远处电势为零,则有( ) 如图所示,真空中有两个静止点电荷,Q=+2×10-4C,q=-2×10-5C,它们相距r=2m,求:
如图所示,真空中有两个静止点电荷,Q=+2×10-4C,q=-2×10-5C,它们相距r=2m,求: 如图所示,真空中有两个固定的点电荷Q1=4.0×10-8C和Q2=8.0×10-8C.求它们连线上P点的场强的大小和方向.
如图所示,真空中有两个固定的点电荷Q1=4.0×10-8C和Q2=8.0×10-8C.求它们连线上P点的场强的大小和方向.