Question

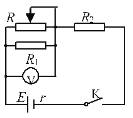
【题目】静止在水平面上的小车固定在刚性水平轻杆的一端，杆的另一端通过小圆环套在竖直光滑的立柱上。每当小车停止运动时，车上的弹簧枪就会沿垂直于轻杆的水平方向自动发射一粒弹丸，然后自动压缩弹簧并装好一粒弹丸等待下次发射，直至射出所有弹丸。下图为该装置的俯视图。已知未装弹丸的小车质量为M，每粒弹丸的质量为m，每次发射弹丸释放的弹性势能为E，发射过程时间极短：小车运动时受到一个与运动方向相反、大小为小车对地面压力λ倍的作用力；忽略所有摩擦阻力，重力加速度为g。

(1)若小车上只装一粒弹丸，求弹丸被射出时小车的速度大小；

(2)若(l)问中发射弹丸后小车恰能运动一周，求射出弹丸时，杆对小车的拉力大小；

(3)若小车上共装25粒弹丸，轻杆能承受的最大拉力 (L为小车做圆周运动的半径），则须满足什么条件轻杆才不会被拉断？小车做圆周运动的总路程的最大值是多少？

Answer 1

【答案】(1) (2) (3) ，

【解析】

（1）对弹丸和小车的系统，发射弹丸的瞬时满足动量守恒和能量守恒，列式求解弹丸被射出时小车的速度大小；（2）根据动能定理求解刚发射完弹丸时小车的速度，根据拉力等于向心力求解杆的拉力；（3）分析发射弹丸的整个过程，可知当弹丸完全发射完时杆的拉力最大，结合数学知识求解小车做圆周运动的总路程的最大值.

（1）发射弹丸的过程，遵守动量守恒定律和机械能守恒；mu=Mv

E=mu2+Mv2

解得

（2）发射弹丸后，小车做圆周运动，圆周半径为L，由动能定理可得：

x=2πL

弹丸刚被射出时杆受到的拉力：

联立解得F=4πλMg

（3）某次发射后，小车（连同弹簧枪）和车载弹丸的总质量为Mk=km(k从某一较大值开始减小，可取25个值，且k>25)

与上述同理可知：

由此可知，弹丸全部射完，k取最小值M/m时，杆的拉力最大，若此时还能满足，则杆不会被拉断，解得

与上述同理可知，某次发射后到下一次发射前小车做圆周运动的路程：

由此式可知，每发射一粒弹丸后，小车做圆周运动的路程增大一些，因此要小车做圆周运动的总路程最大，k应该取最小的25个值（对应将25粒弹丸全部射出），即应取取k=59、58、……、35，

最大总路程为

解得