题目内容
(18分)如图所示,在![]() 的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向垂直于纸面向里,且B1大于B2,一个带负电、比荷为
的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向垂直于纸面向里,且B1大于B2,一个带负电、比荷为![]() 的粒子从坐标原点O,以速度
的粒子从坐标原点O,以速度![]() 沿
沿![]() 轴负方向射出,粒子重力不计。
轴负方向射出,粒子重力不计。
(1)求粒子在两个磁场中运动的轨道半径;
(2)如果B1=2B2,则粒子再次回到原点时运动了多少时间?
(3)要使该粒子经过一段时间后又经过O点,B1与B2的比值应满足什么条件?
(1)![]() 、
、![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ……)
……)
解析:(18分)①粒子在整个过程的速度大小4更为V ,交替地在![]() 平面内
平面内![]() 磁场区域中做匀速圆周运动;轨迹都是半个圆,圆周运动半径分别为
磁场区域中做匀速圆周运动;轨迹都是半个圆,圆周运动半径分别为 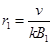 ……①(1分)
……①(1分)
![]() …………………(1分)
…………………(1分)
②当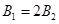 时,
时,![]() ………………(1分)
………………(1分)
那么粒子在左边运动一个半径为![]() 半圆后,再到右边经历一个半径为
半圆后,再到右边经历一个半径为![]() 半圆,又回到左边再找一个半径为
半圆,又回到左边再找一个半径为![]() 半圆的,此时正好回到原点,这个过程中经历的时间为
半圆的,此时正好回到原点,这个过程中经历的时间为
![]() ………………(2分)
………………(2分)
![]() …………………(2分)
…………………(2分)
所以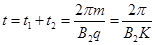 …………………………(1分)
…………………………(1分)
③粒子运动轨迹如图示,
在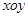 平面内,粒子先沿半径为
平面内,粒子先沿半径为![]() 的半圆
的半圆![]() 运动至
运动至![]() 轴上到
轴上到![]() 点距离为
点距离为![]() 的A 点,接着沿半径为
的A 点,接着沿半径为![]() (
(![]() >
>![]() )的半圆
)的半圆![]() 运动至
运动至![]() 轴上的
轴上的![]() 点,则
点,则![]() 与
与![]() 的距离为:
的距离为:![]() …………(3分)此后粒子每经历一次回旋,其
…………(3分)此后粒子每经历一次回旋,其![]() 轴坐标就减小
轴坐标就减小![]() ,设粒子经过
,设粒子经过![]() 次回旋后与
次回旋后与![]() 轴交于
轴交于![]() 点,若
点,若![]() 即
即![]() 满足
满足![]() ……(3分)
……(3分)
则粒子再经过半圆 就能通过原点,或中
就能通过原点,或中![]() ……为回旋次数。由上得
……为回旋次数。由上得
![]() ……(2分)
……(2分)![]() ……)…………(2分)
……)…………(2分)

练习册系列答案
相关题目
 如图所示,在空间区域Ⅰ存在垂直纸面向里的磁感应强度为B=10T的匀强磁场,其边界为MN、PQ,其中PQ边界位置可以左右调节.在PQ右边空间区域Ⅱ存在水平向右的匀强电场,E=
如图所示,在空间区域Ⅰ存在垂直纸面向里的磁感应强度为B=10T的匀强磁场,其边界为MN、PQ,其中PQ边界位置可以左右调节.在PQ右边空间区域Ⅱ存在水平向右的匀强电场,E=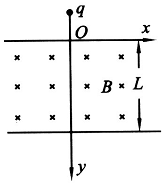
 的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向垂直于纸面向里,且B1大于B2,一个带负电、比荷为
的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向垂直于纸面向里,且B1大于B2,一个带负电、比荷为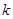 的粒子从坐标原点O,以速度
的粒子从坐标原点O,以速度 沿
沿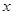 轴负方向射出,粒子重力不计。
轴负方向射出,粒子重力不计。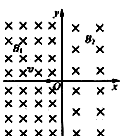
 的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向垂直于纸面向里,且B1大于B2,一个带负电、比荷为
的区域中,存在磁感应强度大小分别为B1与B2的匀强磁场,磁场方向垂直于纸面向里,且B1大于B2,一个带负电、比荷为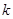 的粒子从坐标原点O,以速度
的粒子从坐标原点O,以速度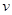 沿
沿 轴负方向射出,粒子重力不计。
轴负方向射出,粒子重力不计。