题目内容
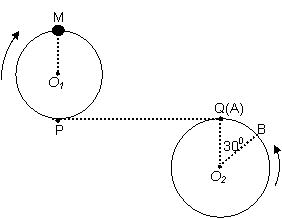
 如图所示,O1为一根长L=0.4m的绳子系一个质量m=2kg的小球在竖直平面内顺时针做圆周运动的圆心,M为最高点,P为最低点,O2为一个绕其逆时针做匀速圆周运动的圆环的圆心,最高点为Q,圆环边缘上有两点A、B,弧AB所对的圆心角为30°,PQ=3.2m且与两个圆相切,当小球运动到M点时,绳子突然断开,此时圆环上的A点也转到了Q点,经过一段时间后,小球恰好落在了Q点,而此时30°圆心角所对弧AB上的某点(不包含A、B两点)也转到了Q点,期间圆环至少转了一圈,(忽略空气阻力,取g=10m/s2)求:
如图所示,O1为一根长L=0.4m的绳子系一个质量m=2kg的小球在竖直平面内顺时针做圆周运动的圆心,M为最高点,P为最低点,O2为一个绕其逆时针做匀速圆周运动的圆环的圆心,最高点为Q,圆环边缘上有两点A、B,弧AB所对的圆心角为30°,PQ=3.2m且与两个圆相切,当小球运动到M点时,绳子突然断开,此时圆环上的A点也转到了Q点,经过一段时间后,小球恰好落在了Q点,而此时30°圆心角所对弧AB上的某点(不包含A、B两点)也转到了Q点,期间圆环至少转了一圈,(忽略空气阻力,取g=10m/s2)求:(1)绳子断开时,小球的速度大小是多少?
(2)小球经过M点时,绳子断开前一瞬间,绳子上的拉力大小是多少?
(3)圆环逆时针做匀速圆周运动的角速度ω应该满足什么条件?
分析:(1)由题意知绳子断开后小球从M点开始做平抛运动,根据平抛运动的基本公式即可求解;
(2)根据向心力公式列式即可求解;
(3)如果在t的时间内,圆环转了n圈后A和Q点重合,则有:nTA=t,如果在t时间内,圆环转了n+
圈后B与Q点重合,则有:(n+
)TB=t,得出周期,求出角速度,注意周期性.
(2)根据向心力公式列式即可求解;
(3)如果在t的时间内,圆环转了n圈后A和Q点重合,则有:nTA=t,如果在t时间内,圆环转了n+
| 1 |
| 12 |
| 1 |
| 12 |
解答:解:(1)由题意知绳子断开后小球从M点开始做平抛运动,从M到Q平抛的时间为:
t=
=
=0.4s
则:PQ=3.2m=v0t=v0×0.4s
得:v0=
=8m/s
(2)绳子断开瞬间在M点的瞬时线速度为:v0=8m/s,
小球在M点做圆周运动的向心力Fn=F+mg=m
得:F=2×
-20=300N
(3)如果在t=0.4s的时间内,圆环转了n圈后A和Q点重合,则有:
nTA=0.4S (n=1,2,3,…)
得周期:TA=
(n=1,2,3,…)
则角速度ωA=
=5nπ(n=1,2,3,…)
如果在t=0.4s的时间内,圆环转了n+
圈后B与Q点重合,则有:
(n+
)TB=0.4s(n=1,2,3,…)
得周期:TB=
s(n=1,2,3,…)
则角速度ωB=5nπ+
π(n=1,2,3,…)
则角度度应该满足的条件是:5nπ<ω<5nπ+
π(n=1,2,3,…)
答:(1)绳子断开时,小球的速度大小是8m/s;
(2)小球经过M点时,绳子断开前一瞬间,绳子上的拉力大小是300N;
(3)圆环逆时针做匀速圆周运动的角速度ω应该满足5nπ<ω<5nπ+
π(n=1,2,3,…).
t=
|
|
则:PQ=3.2m=v0t=v0×0.4s
得:v0=
| 3.2 |
| 0.4 |
(2)绳子断开瞬间在M点的瞬时线速度为:v0=8m/s,
小球在M点做圆周运动的向心力Fn=F+mg=m
| v02 |
| L |
得:F=2×
| 64 |
| 0.4 |
(3)如果在t=0.4s的时间内,圆环转了n圈后A和Q点重合,则有:
nTA=0.4S (n=1,2,3,…)
得周期:TA=
| 2 |
| 5n |
则角速度ωA=
| 2π |
| TA |
如果在t=0.4s的时间内,圆环转了n+
| 1 |
| 12 |
(n+
| 1 |
| 12 |
得周期:TB=
| 24 |
| 60n+5 |
则角速度ωB=5nπ+
| 5 |
| 12 |
则角度度应该满足的条件是:5nπ<ω<5nπ+
| 5 |
| 12 |
答:(1)绳子断开时,小球的速度大小是8m/s;
(2)小球经过M点时,绳子断开前一瞬间,绳子上的拉力大小是300N;
(3)圆环逆时针做匀速圆周运动的角速度ω应该满足5nπ<ω<5nπ+
| 5 |
| 12 |
点评:本题主要考查了圆周运动向心力公式及平抛运动的基本公式的直接应用,要求同学们能正确分析物体的运动情况,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

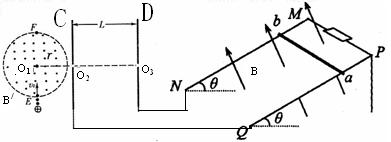
 、圆心为O1的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一坚直放置的平行金属板C和D,两板间距离为L,在MN板中央各有一个小
、圆心为O1的虚线所围的圆形区域内存在垂直纸面向外的匀强磁场,在磁场右侧有一坚直放置的平行金属板C和D,两板间距离为L,在MN板中央各有一个小 孔O2、O3。O1、O2、O3在同一水平直线上,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距也为L。M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直,闭合回路(导轨与导体棒的电阻不计)。整套装置处于匀强磁场中,磁场的磁感应强度为B,磁场方向垂直于斜面向上。整个装置处在真空室中,有一电荷量为+q、质量为m的粒子(重力不计),以速率v0从圆形磁场边界上的最低点
孔O2、O3。O1、O2、O3在同一水平直线上,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距也为L。M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直,闭合回路(导轨与导体棒的电阻不计)。整套装置处于匀强磁场中,磁场的磁感应强度为B,磁场方向垂直于斜面向上。整个装置处在真空室中,有一电荷量为+q、质量为m的粒子(重力不计),以速率v0从圆形磁场边界上的最低点 沿半径方向射入圆形磁场区域,最后从小孔O3射出。现释放导体棒ab,其沿着斜面下滑
沿半径方向射入圆形磁场区域,最后从小孔O3射出。现释放导体棒ab,其沿着斜面下滑 后开始匀速运动,此时仍然从
后开始匀速运动,此时仍然从 从圆形磁场的最高点F射出。求:
从圆形磁场的最高点F射出。求: