题目内容
1. 如图所示,两颗“近地”卫星1和2都绕地球做匀速圆周运动,卫星2的轨道半径更大些.两颗卫星相比较,下列说法中正确的是( )
如图所示,两颗“近地”卫星1和2都绕地球做匀速圆周运动,卫星2的轨道半径更大些.两颗卫星相比较,下列说法中正确的是( )| A. | 卫星2的向心加速度较大 | B. | 卫星2的线速度较大 | ||
| C. | 卫星2的周期较大 | D. | 卫星1的角速度较大 |
分析 卫星绕地球做圆周运动,万有引力提供向心力,由牛顿第二定律求出向心加速度、线速度、周期与角速度,然后分析答题.
解答 解:卫星绕地球做圆周运动,万有引力提供向心力;
A、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=ma,解得:a=$\frac{GM}{{r}^{2}}$,轨道半径r越大,向心加速度a越小,卫星2的轨道半径更大些,卫星2的向心加速度较小,故A错误;
B、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,轨道半径r越大,线速度v越小,卫星2的轨道半径更大些,卫星2的线速度较小,故B错误;
C、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,轨道半径r越大,周期T越大,卫星2的轨道半径更大些,卫星2的周期较大,故C正确;
D、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=mω2r,解得:ω=$\sqrt{\frac{GM}{{r}^{3}}}$,轨道半径r越大,角速度越小,卫星2的轨道半径更大些,卫星2的角速度较小,故D错误;
故选:C.
点评 本题考查了万有引力定律的应用,万有引力提供向心力,应用万有引力公式与牛顿第二定律即可解题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
9.关于磁通量,下列哪个说法是正确的( )
| A. | 穿过某一面积的磁感线条数叫做穿过这个面积的磁通量 | |
| B. | 穿过单位面积的磁感线条数与该面积的比值,叫做穿过这个面积的磁通量 | |
| C. | 某一面积与该处磁感强度的乘积,叫做穿过这个面积的磁通量 | |
| D. | 垂直穿过某一面积的磁感线条数与该面积的比值,叫做穿过这个面积的磁通量 |
16.在图所示电路中各个电阻都是2Ω.电流表内阻不计,在B、C两点间加6V电压时,电流表的读数是( )


| A. | 0 | B. | 1A | C. | 2A | D. | 3A |
13. 如图所示,空间中有一个静止不动的带正电的点电荷,有一带电粒子只在电场力的作用下沿着PSQ轨迹运动.则下列说法中正确的是( )
如图所示,空间中有一个静止不动的带正电的点电荷,有一带电粒子只在电场力的作用下沿着PSQ轨迹运动.则下列说法中正确的是( )
 如图所示,空间中有一个静止不动的带正电的点电荷,有一带电粒子只在电场力的作用下沿着PSQ轨迹运动.则下列说法中正确的是( )
如图所示,空间中有一个静止不动的带正电的点电荷,有一带电粒子只在电场力的作用下沿着PSQ轨迹运动.则下列说法中正确的是( )| A. | 该粒子带正点 | |
| B. | 粒子在P 点的速度比在S 点的速度大 | |
| C. | 粒子在S点的加速度比在Q点的加速度大 | |
| D. | 场源电荷在P点产生的电场强度比在Q点的电场强度大 |
11. 如图所示,滑轮本身的质量忽略不计,滑轮O安装在一根轻木杆上,A端固定在墙上,且保持水平.一根轻绳BC绕过滑轮挂一重物,BC与水平方向夹角为θ,系统保持平衡.若保持滑轮的位置不变,改变θ角的大小,则滑轮受到细绳的弹力大小变化情况是( )
如图所示,滑轮本身的质量忽略不计,滑轮O安装在一根轻木杆上,A端固定在墙上,且保持水平.一根轻绳BC绕过滑轮挂一重物,BC与水平方向夹角为θ,系统保持平衡.若保持滑轮的位置不变,改变θ角的大小,则滑轮受到细绳的弹力大小变化情况是( )
 如图所示,滑轮本身的质量忽略不计,滑轮O安装在一根轻木杆上,A端固定在墙上,且保持水平.一根轻绳BC绕过滑轮挂一重物,BC与水平方向夹角为θ,系统保持平衡.若保持滑轮的位置不变,改变θ角的大小,则滑轮受到细绳的弹力大小变化情况是( )
如图所示,滑轮本身的质量忽略不计,滑轮O安装在一根轻木杆上,A端固定在墙上,且保持水平.一根轻绳BC绕过滑轮挂一重物,BC与水平方向夹角为θ,系统保持平衡.若保持滑轮的位置不变,改变θ角的大小,则滑轮受到细绳的弹力大小变化情况是( )| A. | 只有θ变小,弹力才变大 | B. | 只有θ变大,弹力才变大 | ||
| C. | 不论θ变小或变大,弹力都变大 | D. | 不论θ如何变化,弹力都不变 |
 如图所示,OO′上侧有磁感应强度大小B=2.0×10-4T的匀强磁场,电子以V=1.6×106m/s的速度从A点与OO′垂直的方向进入磁场,在垂直于磁场的平面内运动.已知电子质量m=9.1×10-31kg、电量q=1.6×10-19C.
如图所示,OO′上侧有磁感应强度大小B=2.0×10-4T的匀强磁场,电子以V=1.6×106m/s的速度从A点与OO′垂直的方向进入磁场,在垂直于磁场的平面内运动.已知电子质量m=9.1×10-31kg、电量q=1.6×10-19C.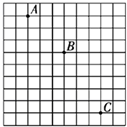 图为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,求
图为一小球做平抛运动的闪光照相照片的一部分,图中背景方格的边长均为5cm,如果取g=10m/s2,求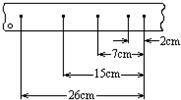 如图所示的纸带是由斜面下滑的小车通过打点计时器拉出来的,打点的时间间隔是0.02s,现按每10个点划分纸带,数据已标在图上,打点计时器打下第二个点是小车的速度为0.175m/s,小车运动的加速度为0.75m/s2.
如图所示的纸带是由斜面下滑的小车通过打点计时器拉出来的,打点的时间间隔是0.02s,现按每10个点划分纸带,数据已标在图上,打点计时器打下第二个点是小车的速度为0.175m/s,小车运动的加速度为0.75m/s2.