题目内容
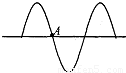
一列简谐横波沿水平直线方向向右传播．M、N为介质中相距为s的两质点，M在左，N在右，某时刻M、N两质点振动正好经过平衡位置，而且M、N之间只有一个波峰，经过t时间N质点恰好处于波峰位置，求这列波的波速．?
分析：根据某时刻M、N两质点振动正好经过平衡位置及M、N之间只有一个波峰的事实，可以画出M、N间可能的波形如图所示，由图可求出波长λ．再根据t时间内质点N由平衡位置恰好到达波峰位置的事实，又可求出质点振动的周期T．由公式v=
就可以求出这列波的波速v．?
| λ |
| T |
解答：解：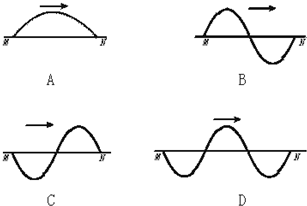
在A图中，λA=2s．由于此时刻N质点正在经过平衡位置向上运动（用“右右上”判断），且经过t时间到达波峰位置，因此t=
+nTA，所以TA=
?
vA=
=
（n=0，1，2…）?
在B图中，λB=s．由于此时刻N质点正在经过平衡位置向下振动，且经过t时间到达波峰位置．因此t=
TB+nTB，所以TB=
．
vB=
=
（n=0，1，2…）?
在C图中，λC=s，t=
+nTC，Tc=
，所以?
vC=
=
（n=0，1，2…）?
在D图中，
λD=s，t=
TD+nTD，TD=
，所以?
vD=
=
（n=0，1，2…）?
答：波速可能为
（n=0，1，2…）、
（n=0，1，2…）、
（n=0，1，2…）、
（n=0，1，2…）．
在A图中，λA=2s．由于此时刻N质点正在经过平衡位置向上运动（用“右右上”判断），且经过t时间到达波峰位置，因此t=
| TA |
| 4 |
| 4t |
| 4n+1 |
vA=
| λA |
| TA |
| (4n+1)s |
| 2t |
在B图中，λB=s．由于此时刻N质点正在经过平衡位置向下振动，且经过t时间到达波峰位置．因此t=
| 3 |
| 4 |
| 4t |
| 4n+3 |
vB=
| λB |
| TB |
| (4n+3)s |
| 4t |
在C图中，λC=s，t=
| TC |
| 4 |
| 4t |
| 4n+1 |
vC=
| λC |
| TC |
| (4n+1)s |
| 4t |
在D图中，
| 3 |
| 2 |
| 3 |
| 4 |
| 4t |
| 4n+1 |
vD=
| λD |
| TD |
| (4n+1)s |
| 6t |
答：波速可能为
| (4n+1)s |
| 2t |
| (4n+3)s |
| 4t |
| (4n+1)s |
| 4t |
| (4n+1)s |
| 6t |
点评：解决本题的关键确定出M、N间只有一个波峰的可能情况，结合波速、波长、周期的关系，运用波的周期性进行求解．
练习册系列答案
相关题目
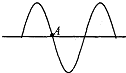如图所示为一列简谐横波沿水平直线传播时某时刻的波形图，其波长为4m，若图中A点经过0.5s第一次到达下方最大位移处，以下说法正确的是（ ）