题目内容
一列简谐横波沿水平直线方向向右传播,M、N为介质中相距为Δs的两质点,M在左,N在右,t时刻,M、N两质点正好振动经过平衡位置,而且M、N之间只有一个波峰,经过Δt时间N质点恰处在波峰位置,求这列波的波速.
![]()
![]()
![]()
![]()
解析:
设波的波长为λ,周期为T,由题意可知,M、N两质点的距离Δs可能等于![]() ,或等于λ或等于
,或等于λ或等于![]() ,且M、N均过平衡位置的时刻其波形为如图7四种情况
,且M、N均过平衡位置的时刻其波形为如图7四种情况

图7
对(a),N质点正在经过平衡位置向上振动,已知N经过时间Δt到达波峰位置,则Δt可能为![]() 、
、![]() 、
、![]() ……即Δt可能为Δt=(k+
……即Δt可能为Δt=(k+![]() )T(k=0,1,2,…)由
)T(k=0,1,2,…)由![]() ,并且考虑到λ=2Δs,可得
,并且考虑到λ=2Δs,可得![]() (k=0,1,2,…)
(k=0,1,2,…)
对于(b),N质点正在经过平衡位置向下振动,已知N经过时间Δt到达波峰位置,则Δt可能为![]() 、
、![]() 、
、![]() ……即Δt可能为t=(k+
……即Δt可能为t=(k+![]() )T,(k=0,1,2,…)由
)T,(k=0,1,2,…)由![]() ,并且考虑到λ=Δs,可得
,并且考虑到λ=Δs,可得![]() (k=0,1,2,…)同理,(c)(d)分别有
(k=0,1,2,…)同理,(c)(d)分别有![]() (k=0,1,2,…)和
(k=0,1,2,…)和![]() (k=0,1,2,…)
(k=0,1,2,…)
由此我们可以看到该题的四组通解.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
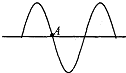 如图所示为一列简谐横波沿水平直线传播时某时刻的波形图,其波长为4m,若图中A点经过0.5s第一次到达下方最大位移处,以下说法正确的是( )
如图所示为一列简谐横波沿水平直线传播时某时刻的波形图,其波长为4m,若图中A点经过0.5s第一次到达下方最大位移处,以下说法正确的是( )