题目内容
(10分)滑雪运动中当滑雪板压在雪地时会把雪内的空气逼出来,在滑雪板与雪地间形成一个
暂时的“气垫”,从而大大减小雪地对滑雪板的摩擦,然而当滑雪板相对雪地速度较小时,与雪地接触时间
超过某一值就会陷下去,使得它们间的摩擦力增大。假设滑雪者的速度超过4m/s时,滑雪板与雪地间的动
摩擦因数就会由μ1=0.25变为μ2=0.125。一滑雪者从倾角θ=37°的坡顶A处由静止开始自由下滑,滑至坡
底B(B处为一光滑小圆弧)后又滑上一段水平雪地,最后停在C处,如图所示,不计空气阻力,坡长L=26m,取g=10m/s2,sin37°=0.6,cos37°=0.8,求:
(1)滑雪者从静止开始到动摩擦因数发生变化所经历的时间;
(2)滑雪者到达B处的速度大小;
(3)滑雪者在水平雪地上运动的最大距离。
(1)1s (2)16m/s (3)99.2m
解析试题分析:(1)设滑雪者质量为m,滑雪者在斜坡上从静止开始加速至速度v1=4m/s期间,由牛顿第二定律: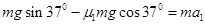 (1分)
(1分)
解得: (1分)
(1分)
故由静止开始到动摩擦因数发生变化所经历的时间: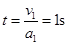 (1分)
(1分)
(2)根据牛顿定律和运动学公式有: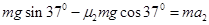 (1分)
(1分)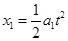 (1分)
(1分)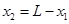 (1分)
(1分)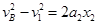 (1分)
(1分)
代入数据解得: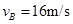 (1分)
(1分)
(3)设滑雪者速度由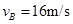 减速到
减速到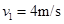 期间运动的位移为
期间运动的位移为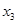 ,速度由
,速度由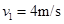 减速到零期间运动的位移为
减速到零期间运动的位移为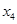 ,则由动能定理有:
,则由动能定理有: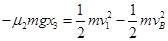 ,解得
,解得 (1分)
(1分)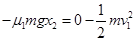 ,解得
,解得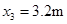 (1分)
(1分)
所以滑雪者在水平雪地上运动的最大距离为: (1分)
(1分)
考点:本题考查了牛顿运动定律和匀变速直线运动规律的应用。

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目

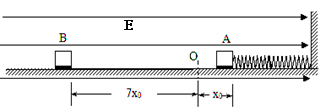
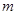 电荷量
电荷量 的与外界绝缘物块A(可视为质点),置于光滑水平面上。A与弹簧左端相连接,弹簧右端固定在竖直墙面上,整个空间中存在水平向右的匀强电场,场强
的与外界绝缘物块A(可视为质点),置于光滑水平面上。A与弹簧左端相连接,弹簧右端固定在竖直墙面上,整个空间中存在水平向右的匀强电场,场强 ,平衡时弹簧的压缩量为
,平衡时弹簧的压缩量为 .如图O为弹簧原长时的位置,另一个质量也为
.如图O为弹簧原长时的位置,另一个质量也为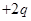 的绝缘带电物块B(可视为质点),从O点左侧距离O为
的绝缘带电物块B(可视为质点),从O点左侧距离O为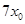 处的P点由静止释放,当它打在A物块上时立即与A一起向右运动,但不粘连,它们到达最右端后又向左运动,试求:物块B向左运动达到最远点时距O点的距离?(AB相撞在瞬间完成,电荷无转移,不计AB间库仑力,弹簧始终在弹性限度内)。
处的P点由静止释放,当它打在A物块上时立即与A一起向右运动,但不粘连,它们到达最右端后又向左运动,试求:物块B向左运动达到最远点时距O点的距离?(AB相撞在瞬间完成,电荷无转移,不计AB间库仑力,弹簧始终在弹性限度内)。