题目内容
为了抗议美国、韩国在我国领海附近的联合军事演习,2010年7月~8月份,我空军某部多次在东海、黄海进行军事演练,在一次低空跳伞训练中,当直升飞机悬停在离地面224m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵以12.5m/s2的加速度匀减速下降.为了伞兵的安全,要求伞兵落地速度最大不得超过5m/s,(取g=10m/s2)求:(1)伞兵展伞时,离地面的高度至少为多少?着地时相当于从多高处自由落下?
(2)伞兵在空中的最短时间为多少?

【答案】分析:(1)整个过程中,伞兵先做自由落体运动,后做匀减速运动,总位移大小等于224m.设伞兵展伞时,离地面的高度至少为h,此时速度为v,先研究匀减速过程,由速度-位移关系式,得到v与h的关系式,再研究自由落体过程,也得到一个v与h的关系式,联立求解.
(2)由(1)求出v,由速度公式求出两个过程的时间,即可得到总时间.
解答:解:(1)设伞兵展伞时,离地面的高度至少为h,此时速度为v,
则:
对于匀减速运动过程,有 v2-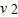 =-2ah,
=-2ah,
即52-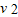 =-2×12.5×h
=-2×12.5×h
对于自由下落过程,有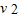 =2g(224-h)=2×10×(224-h)
=2g(224-h)=2×10×(224-h)
联立解得h=99 m,v=50 m/s
以5m/s的速度落地相当于从h1高处自由落下,
即2gh1=v2 所以h1=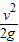 =
= m=1.25 m.
m=1.25 m.
(2)设伞兵在空中的最短时间为t,
则有v=gt1,t1=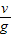 =
=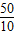 s=5 s,
s=5 s,
t2=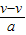 =
=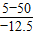 s=3.6 s,
s=3.6 s,
故所求时间t=t1+t2=(5+3.6)s=8.6 s.
答:(1)伞兵展伞时,离地面的高度至少为99m,着地时相当于从1.25m高处自由落下.
(2)伞兵在空中的最短时间为8.6s.
点评:本题涉及两个过程的运动学问题,既要单独研究两个过程,更要抓住它们之间的联系:比如位移关系、速度关系等等.
(2)由(1)求出v,由速度公式求出两个过程的时间,即可得到总时间.
解答:解:(1)设伞兵展伞时,离地面的高度至少为h,此时速度为v,
则:
对于匀减速运动过程,有 v2-
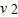 =-2ah,
=-2ah,即52-
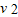 =-2×12.5×h
=-2×12.5×h对于自由下落过程,有
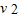 =2g(224-h)=2×10×(224-h)
=2g(224-h)=2×10×(224-h)联立解得h=99 m,v=50 m/s
以5m/s的速度落地相当于从h1高处自由落下,
即2gh1=v2 所以h1=
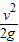 =
= m=1.25 m.
m=1.25 m.(2)设伞兵在空中的最短时间为t,
则有v=gt1,t1=
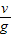 =
=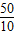 s=5 s,
s=5 s,t2=
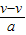 =
=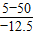 s=3.6 s,
s=3.6 s,故所求时间t=t1+t2=(5+3.6)s=8.6 s.
答:(1)伞兵展伞时,离地面的高度至少为99m,着地时相当于从1.25m高处自由落下.
(2)伞兵在空中的最短时间为8.6s.
点评:本题涉及两个过程的运动学问题,既要单独研究两个过程,更要抓住它们之间的联系:比如位移关系、速度关系等等.

练习册系列答案
相关题目
 为了抗议美国、韩国在我国领海附近的联合军事演习,2010年7月~8月份,我空军某部多次在东海、黄海进行军事演练,在一次低空跳伞训练中,当直升飞机悬停在离地面224m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵以12.5m/s2的加速度匀减速下降.为了伞兵的安全,要求伞兵落地速度最大不得超过5m/s,(取g=10m/s2)求:
为了抗议美国、韩国在我国领海附近的联合军事演习,2010年7月~8月份,我空军某部多次在东海、黄海进行军事演练,在一次低空跳伞训练中,当直升飞机悬停在离地面224m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵以12.5m/s2的加速度匀减速下降.为了伞兵的安全,要求伞兵落地速度最大不得超过5m/s,(取g=10m/s2)求: 为了抗议美国、韩国在我国领海附近的联合军事演习,2010年7月~8月份,我空军某部多次在东海、黄海进行军事演练,在一次低空跳伞训练中,当直升飞机悬停在离地面180m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵所受阻力恒为重力的0.218倍.为了伞兵的安全,要求伞兵落地速度最大不得超过6m/s,(取g=10m/s2)求:
为了抗议美国、韩国在我国领海附近的联合军事演习,2010年7月~8月份,我空军某部多次在东海、黄海进行军事演练,在一次低空跳伞训练中,当直升飞机悬停在离地面180m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵所受阻力恒为重力的0.218倍.为了伞兵的安全,要求伞兵落地速度最大不得超过6m/s,(取g=10m/s2)求: 为了抗议美国、韩国在我国领海附近的联合军事演习,2010年7月~8月份,我空军某部多次在东海、黄海进行军事演练,在一次低空跳伞训练中,当直升飞机悬停在离地面180m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵所受阻力恒为重力的0.218倍.为了伞兵的安全,要求伞兵落地速度最大不得超过6m/s,(取g=10m/s2)求:
为了抗议美国、韩国在我国领海附近的联合军事演习,2010年7月~8月份,我空军某部多次在东海、黄海进行军事演练,在一次低空跳伞训练中,当直升飞机悬停在离地面180m高处时,伞兵离开飞机做自由落体运动.运动一段时间后,打开降落伞,展伞后伞兵所受阻力恒为重力的0.218倍.为了伞兵的安全,要求伞兵落地速度最大不得超过6m/s,(取g=10m/s2)求: