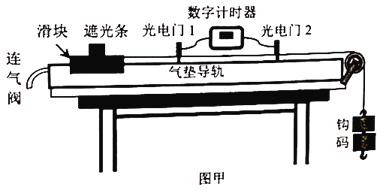
题目内容
【题目】如图所示，倾斜轨道AB和光滑圆弧轨道BC固定在同一竖直平面内，两者间通过一小段长度不计的光滑弧形轨道相连，已知AB长L＝7.80 m，倾角
＝37°，BC弧的半径R＝0.8 m，O为圆心，∠BOC＝143°．整个装置处于水平向左的匀强电场中(图中未画出)，电场强度大小E＝1×103 N／C．两个相同的绝缘小球P和Q，质量均为m＝0.4 kg，带正电的小球Q静止在A点，其带电荷量q＝3×10－3C，不带电的小球P从某一位置以v0＝8 m／s的初速度水平抛出，运动到A点时恰好沿斜面向下与小球Q发生弹性正碰，且碰撞过程无电荷转移．若Q、P与轨道AB间的动摩擦因数分别为
＝0.2和
＝0.8，sin 37°＝0.6，cos37＝0.8，g取10 m／s2，小球Q运动过程中电荷量保持不变．求：
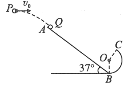
(1)小球P的抛出点距A点的高度；
(2)小球Q运动到圆弧轨道最低点B点时对轨道的压力；
(3)小球Q离开圆轨道后，第一次落到斜面上的位置距B点的距离．
【答案】(1) 
(2) 
(3) 
【解析】
（1）小球P抛出后做平抛运动，到达A点时速度沿斜面向下，由速度分解法求出小球P到达A点时竖直分速度，即可由运动学公式求出小球P的抛出点距A点的高度；
（2）两球发生弹性正碰，由动量守恒定律和机械能守恒定律结合求出碰后两球的速度。碰后小球Q获得速度，将电场力和重力的合力看成等效重力，由动能定理求出小球Q到圆弧轨道最低点B点时的速度，由牛顿运动定律求Q对轨道的压力；
（3）假设小球Q能到达C点，由动能定理求得到达C点的速度，与临界速度比较，判断知道小球Q能到达C点。小球Q离开轨道后做类平抛运动，运用分位移公式求解Q第一次落到斜面上的位置距B点的距离。
（1）设小球P刚运动到A点时的速度为vA，竖直分速度为vAy．则有：
vAy=v0tan37°=8×
=6m/s
所以小球P的抛出点距A点的高度为：
（2）P、Q碰撞过程，动量守恒、机械能守恒。设碰后P、Q的速度分别为vP、vQ。
取沿斜面向下为正方向，由动量守恒定律和机械能守恒定律得：mvA=mvP+mvQ；
mvA2=mvP2+ mvQ2；
解得：vP=0，vQ=10m/s
碰后小球Q受到的电场力 qE=3N，方向水平向左，且与重力的合力大小为5N，方向垂直于AB斜面向下，则“等效重力场”的等效重力加速度 g′=
g=12.5m/s2，方向垂直AB斜面向下。
设小球A滑到B点时的速度为vB。
由动能定理得：-μmg′l=mvB2 - mvQ2
解得：vB=
m/s
对小球Q，在B点，由牛顿第二定律得：N-mg=m
解得：N=34.5N
由牛顿第三定律知，小球Q运动到圆弧轨道最低点B点时对轨道的压力也为34.5N。
（3）设小球Q能到达C点，且在C点的速度为vC．则小球Q从A到C的过程中，由动能定理得：
-μmg′l-mg′R（1+cos37°）= mvC2-mvQ2
解得：vC=5m/s
设小球Q恰好到C点时的速度为v′C，则有：mg′=m
解得：v′C=
m/s
因vC＞v′C，所以小球能到达C点，小球Q离开C后，做类平抛运动，则有：
x′=vCt
R+Rcos37°=g′t2
解得：t=
s，x′≈2.4m
故小球Q的落点距B点的距离为：x=x′+Rsin37°=2.4+0.8×0.6=2.88m
