题目内容
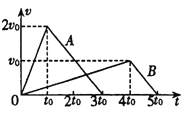
【题目】“30m折返跑”中.在平直的跑道上,一学生站立在起点线处,当听到起跑口令后(测试员同时开始计时),跑向正前方30m处的折返线,到达折返线处时,用手触摸固定的折返处的标杆,再转身跑回起点线,到达起点线处时,停止计时,全过程所用时间即为折返跑的成绩.学生可视为质点,加速或减速过程均视为匀变速,触摸杆的时间不计.该学生加速时的加速度大小为a1=2.5m/s2,减速时的加速度大小为a2=5m/s2,到达折返线处时速度需减小到零,并且该学生全过程最大速度不超过Vm=12m/s.求该学生“30m折返跑”的最好成绩.
【答案】10.9s
【解析】
试题分析:设起点纸处为A,折返线处为B,该学生从A到B的过程中,先做匀加速运动,紧接着做匀减速直线运动,并设此过程中达到的最大速度为v,做匀加速运动的时间为t1,做匀减速运动的时间为t2,则由运动学公式,有:v=a1t1…①
v=a2t2 …②![]() …③
…③
联立①②③式,可解得:v=10m/s
t1=4s,t2=2s
因为v<vm,所以从A到B的过程中,学生的确先做匀加速运动,然后做匀减速运动.从B到A的加速过程中,速度从零增大到12m/s需用时:![]()
加速过程的位移为:![]()
最后阶段的匀速运动用时:![]()
所以,该学生“30m折返跑”的成绩为:t=t1+t2+t3+t4=10.9s

练习册系列答案
相关题目