题目内容
【题目】如图所示是生产流水线上的皮带传输装置,传输带上等间距地放着很多半成品产品.A轮处装有光电计数器,它可以记录通过A处的产品数目,已测得轮A,B的半径分别为rA=20 cm、rB=10 cm,相邻两产品间的距离为30 cm,1 min内有41个产品通过A处,求:
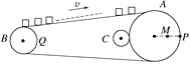
(1)产品随传输带移动的速度大小.
(2)A,B轮边缘上的两点P、Q及A轮半径中点M的线速度和角速度大小,并在图中画出线速度的方向.
(3)如果A轮是通过摩擦带动C轮转动,且rC=5 cm,在图中描出C轮的转动方向,求出C轮的角速度(假设轮不打滑).
【答案】(1)0.2m/s;(2) vP=0.2 m/s vQ=0.2 m/s vM=0.1 m/s ωP=1 rad/s ωQ=2 rad/s ωM=1 rad/s
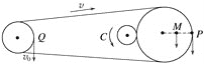
(3) 如图所示 4 rad/s
【解析】试题分析:首先明确产品与传送带保持相对静止的条件下,产品速度的大小就等于传送带上每一点速度的大小,在传送带不打滑的条件下,传送带上各点运动速度的大小都等于A、B轮缘上点的线速度的大小。由传送带相邻产品的间距及单位时间内通过A处的产品的个数可以确定出皮带上点的速度,进而知道A、B轮缘上的两点P、Q线速度的大小,然后由线速度与角速度的关系,求出A、B两轮的角速度及A轮半径中点M的线速度及C轮的角速度.由题意知,1分钟内有41个产品通过A处,说明1分钟内传输带上的每点运动的路程为两产品间距的40倍。
解:(1) 每分钟传送带移动距离:x=40x=40×30×10-2m=12m
产品随传输带移动的速度: ![]() ;
;
(2) 传送带不打滑时,传送带某点的移动速度等于轮缘某点圆周运动的线速度,所以:
vP=vQ=0.2m/s
由于M点与P点角速度相同,且M为A轮半径中点,故
由线速度与角速度的关系![]()
P、M共同角速度为![]()
Q点角速度![]()
各点速度方向如图示

(3) 不打滑,两轮边缘某点线速度相等,即:rAω1=rCω3
所以, ![]()
C轮转动方向如上图所示。

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案