题目内容
【题目】间距为 
的两平行金属导轨由水平部分和倾斜部分平滑连接而成，如图所示,倾角为θ的导轨处于大小为 
，方向垂直导轨平面向上的匀强磁场区间Ⅰ中，水平导轨上的无磁场区间静止放置一质量为3 
的“联动双杆”（由两根长为 的金属杆， 
和 
，用长度为L的刚性绝缘杆连接而成），在“联动双杆”右侧存在大小为 
，方向垂直导轨平面向上的匀强磁场区间Ⅱ，其长度大于L，质量为 ，长为 的金属杆 
，从倾斜导轨上端释放，达到匀速后进入水平导轨（无能量损失），杆 与“联动双杆”发生碰撞后杆 和 合在一起形成“联动三杆”，“联动三杆”继续沿水平导轨进入磁场区间Ⅱ并从中滑出，运动过程中，杆 、 和 与导轨始终接触良好，且保持与导轨垂直。已知杆 、 和 电阻均为 
。不计摩擦阻力和导轨电阻，忽略磁场边界效应。求：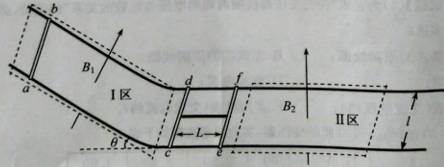
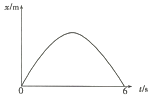
（1）杆 在倾斜导轨上匀速运动时的速度大小 
；
（2）联动三杆进入磁场区间II前的速度大小 
；
（3）联动三杆滑过磁场区间II产生的焦耳热 
【答案】
（1）
感应电动势 
电流 
安培力 
匀速运动条件 
（2）
由动量守恒定律 
（3）
进入B2磁场区域，设速度变化Dv,动量定理有
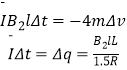
出B2磁场后“联动三杆”的速度为
【解析】（1）ab杆在倾斜轨道上做匀速直线运动，由平衡条件可以求出其速度．（2）ab杆与联动双杆碰撞过程系统动量守恒，应用动量守恒定律可以求出其速度．（3）应用动量定理与能量守恒定律可以求出联动三杆产生的焦耳热．
【考点精析】本题主要考查了动量定理和动量守恒定律的相关知识点，需要掌握动量定理的研究对象可以是单个物体，也可以是物体系统.对物体系统，只需分析系统受的外力，不必考虑系统内力.系统内力的作用不改变整个系统的总动量；动量定理不仅适用于恒定的力，也适用于随时间变化的力.对于变力，动量定理中的力F应当理解为变力在作用时间内的平均值；动量守恒定律成立的条件：系统不受外力或系统所受外力的合力为零；系统所受的外力的合力虽不为零，但系统外力比内力小得多；系统所受外力的合力虽不为零，但在某个方向上的分量为零，则在该方向上系统的总动量的分量保持不变才能正确解答此题．
