题目内容
人造地球卫星所受的向心力与轨道半径r的关系，下列说法中正确的是（ ）A．由
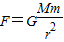可知，向心力与r2成反比B．由
可知，向心力与r成反比C．由F=mw2r可知，向心力与r成正比
D．由F=mwv可知，向心力与r 无关
【答案】分析：人造地球卫星的轨道半径变化时，速度v变化，ω变化，F与r不是反比关系，与ω不是正比关系．
公式F=mωv中，ω、v均与半径R有关，F也与R有关．由公式F=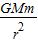
，F和r2成反比，
解答：解：A、人造地球卫星的轨道半径变化时，卫星与地球质量不变，由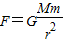
可知，向心力与r2成反比，故A正确
B、人造地球卫星的轨道半径变化时，速度v变化，所以由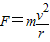
可知，向心力与r成反比是错误的，故B错误
C、公式F=mωv中，ω、v均与半径R有关，所以向心力与r成正比是错误的，故C错误
D、由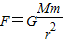
可知，向心力与r2成反比，故D错误
故选A．
点评：本题关键抓住卫星的速度、角速度都与卫星的轨道半径有关，采用控制变量法来理解就行了．
公式F=mωv中，ω、v均与半径R有关，F也与R有关．由公式F=
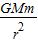，F和r2成反比，解答：解：A、人造地球卫星的轨道半径变化时，卫星与地球质量不变，由
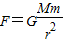可知，向心力与r2成反比，故A正确B、人造地球卫星的轨道半径变化时，速度v变化，所以由
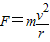可知，向心力与r成反比是错误的，故B错误C、公式F=mωv中，ω、v均与半径R有关，所以向心力与r成正比是错误的，故C错误
D、由
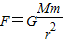可知，向心力与r2成反比，故D错误故选A．
点评：本题关键抓住卫星的速度、角速度都与卫星的轨道半径有关，采用控制变量法来理解就行了．
练习册系列答案
相关题目
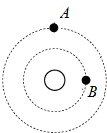某些人造地球卫星的变轨过程可简化为：开始时人造地球卫星在轨道半径较小的轨道B上以速度v1绕地球作匀速圆周运动，然后卫星所携带的发动机喷气，极短时间内喷气结束，使卫星的速度变为v2，卫星又进入轨道转移阶段，向距离地面更高的位置运动，到达预定位置以后，地面控制中心遥控使卫星定位，卫星又绕地球在半径更大的轨道A上以速度v3绕地球作匀速圆周运动，设在轨道A、B上卫星只受地球的万有引力，则v1、v2、v3的大小关系为（ ）
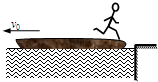A．质量为M的小船上站有一个质量为m的人，船相对于岸以v0的速度在平静的水面上向左缓缓漂动，如图所示．某时刻人以相对于岸向右的速度v水平跳出，则人跳船前后船的动量变化方向是