题目内容
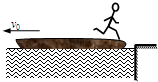 A.质量为M的小船上站有一个质量为m的人,船相对于岸以v0的速度在平静的水面上向左缓缓漂动,如图所示.某时刻人以相对于岸向右的速度v水平跳出,则人跳船前后船的动量变化方向是
A.质量为M的小船上站有一个质量为m的人,船相对于岸以v0的速度在平静的水面上向左缓缓漂动,如图所示.某时刻人以相对于岸向右的速度v水平跳出,则人跳船前后船的动量变化方向是B.两颗人造地球卫星,它们质量之比为1:2,它们运行的线速度之比为1:2,那么它们运行的轨道半径之比为
分析:A、以人与船组成的系统为研究对象,由动量守恒定律可以求出船的速度,然后求出船的动量变化.
B、万有引力提供卫星做圆周运动的向心力,由牛顿第二定律可以求出卫星的轨道半径之比,由向心力公式可以求出向心力之比.
B、万有引力提供卫星做圆周运动的向心力,由牛顿第二定律可以求出卫星的轨道半径之比,由向心力公式可以求出向心力之比.
解答:解:A、以船的初速度方向为正方向,以人与船组成的系统为研究对象,由动量守恒定律可得:
(m+M)v0=-mv+Mv′,
解得:v′=
+v0,
船速度的变化为:△v=v′-v0=
,方向与v0方向相同,向左;
B、万有引力提供卫星做圆周运动所需要的向心力,
设地球质量为M,卫星质量为m,卫星轨道半径为r,
由牛顿第二定律可得:G
=m
,则r=
,
=
=
=(
)2=
;
万有引力提供向心力,向心力之比:
=
=
=
×(
)2=
;
故答案为:A、向左,
;B.4:1,1:32.
(m+M)v0=-mv+Mv′,
解得:v′=
| m(v0+v) |
| M |
船速度的变化为:△v=v′-v0=
| m(v0+v) |
| M |
B、万有引力提供卫星做圆周运动所需要的向心力,
设地球质量为M,卫星质量为m,卫星轨道半径为r,
由牛顿第二定律可得:G
| Mm |
| r2 |
| v2 |
| r |
| GM |
| v2 |
| r1 |
| r2 |
| ||||
|
| ||
|
| 2 |
| 1 |
| 4 |
| 1 |
万有引力提供向心力,向心力之比:
| F1 |
| F2 |
G
| ||||
G
|
m1
| ||
m2
|
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 32 |
故答案为:A、向左,
| m(v+v0) |
| M |
点评:A、应用动量守恒定律即可正确解题,应用动量守恒定律时要注意正方向的选择.
B、万有引力提供卫星做圆周运动的向心力,应用牛顿第二定律即可正确解题.
B、万有引力提供卫星做圆周运动的向心力,应用牛顿第二定律即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【物理——选修3-5】(15分)
【小题1】下列说方法正确的是 ( )
| A.人类关于原子核内部的信息,最早来自天然放射现象 |
| B.在α、β、γ三种射线中γ射线电离作用最强 |
| C.放射性元素的半衰期会随着温度的升高而缩短 |
| D.较重的核分裂成中等质量大小的核或较轻的核合并成中等质量大小的核,核子的比结合能都会增加 |
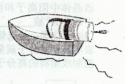
(1)喷射出质量为△m的液体后,小船的速度是多少?
(2)喷射出△m液体的过程中,小船所受气体的平均作用力的大小是多少?
 (2013?嘉定区一模)A设地球半径为R,地球表面的重力加速度为g,若某质量为m的地球同步通讯卫星,离开地面的高度为H,则它绕地球运行时所受的向心力大小为
(2013?嘉定区一模)A设地球半径为R,地球表面的重力加速度为g,若某质量为m的地球同步通讯卫星,离开地面的高度为H,则它绕地球运行时所受的向心力大小为 [物理---选修3-5]
[物理---选修3-5]