题目内容
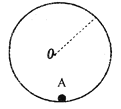
【题目】如图所示，内壁光滑半径大小为R的圆轨道固定在竖直平面内，一个质量为m的小球静止在轨道的最低点A点。现给小球一个瞬时水平打击力，使小球沿轨道在竖直平面内运动。当小球运动重新回到A点时，再沿它的运动方向给第二次瞬时打击力。经过二次击打后，小球才能够通过轨道的最高点，已知第一次和第二次对小球的打击力做的功分别为W和3W，则W的值可能为
A. 
B. 
C. 
D. 
【答案】BCD
【解析】小球在竖直面内运动只有重力做功，故机械能守恒；小球要到达圆轨道最高点，那么对小球在最高点应用牛顿第二定律可得：mg≤
，所以小球的机械能E＝2mgR+
mv2≥
mgR；小球在运动过程中始终未脱离轨道，且必须经过两次击打，小球才能运动到圆轨道的最高点，故第一次击打后，小球运动的高度不大于R，所以有W≤mgR，W+3W≥mgR，
所以，
mgR≤W≤mgR，故BCD正确，A错误；故选BCD．
练习册系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
