题目内容
2.人造地球卫星做半径为r,线速度大小为v的匀速圆周运动.当其角速度变为原来的$\frac{\sqrt{2}}{4}$倍后,运动半径为2r,线速度大小为$\frac{{\sqrt{2}}}{2}$.分析 人造地球卫星做匀速圆周运动,万有引力提供向心力,运用牛顿第二定律列方程求角速度与半径的关系,再运用牛顿第二定律列方程求线速度与半径的关系
解答 解:万有引力提供向心力,得$G\frac{Mm}{{r}^{2}}=m{ω}^{2}r$
解得:$ω=\sqrt{\frac{GM}{{r}^{3}}}$
则$\frac{r′}{r}=\root{3}{\frac{{ω}^{2}}{ω{′}^{2}}}=2$,即r′=2r
故答案为:2r
点评 人造地球卫星做匀速圆周运动,一定要使用万有引力提供向心力的公式来讨论半径与线速度、角速度、周期等的关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.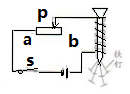 如图是电磁铁工作原理的示意图,由线圈、电源、开关和滑动变阻器等器材组成,P为滑动变阻器的滑片.闭合S,铁钉被吸附起来.下列分析正确的是( )
如图是电磁铁工作原理的示意图,由线圈、电源、开关和滑动变阻器等器材组成,P为滑动变阻器的滑片.闭合S,铁钉被吸附起来.下列分析正确的是( )
 如图是电磁铁工作原理的示意图,由线圈、电源、开关和滑动变阻器等器材组成,P为滑动变阻器的滑片.闭合S,铁钉被吸附起来.下列分析正确的是( )
如图是电磁铁工作原理的示意图,由线圈、电源、开关和滑动变阻器等器材组成,P为滑动变阻器的滑片.闭合S,铁钉被吸附起来.下列分析正确的是( )| A. | 增加线圈匝数,被吸附的铁钉减少 | B. | 调换电源正负极,铁钉不能被吸附 | ||
| C. | P向a端移动,被吸附的铁钉增多 | D. | P向b端移动,被吸附的铁钉增多 |
13.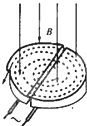 如图所示,回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形盒,两盒间构成一狭缝,两D形盒处于垂直于盒面的匀强磁场中.下列有关回旋加速器的描述正确的是( )
如图所示,回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形盒,两盒间构成一狭缝,两D形盒处于垂直于盒面的匀强磁场中.下列有关回旋加速器的描述正确的是( )
 如图所示,回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形盒,两盒间构成一狭缝,两D形盒处于垂直于盒面的匀强磁场中.下列有关回旋加速器的描述正确的是( )
如图所示,回旋加速器是加速带电粒子的装置,其核心部分是分别与高频交流电源两极相连接的两个D形盒,两盒间构成一狭缝,两D形盒处于垂直于盒面的匀强磁场中.下列有关回旋加速器的描述正确的是( )| A. | 粒子由加速器的边缘进入加速器 | |
| B. | 粒子由加速器的中心附近进入加速器 | |
| C. | 粒子在狭缝和D形盒中运动时都能获得加速 | |
| D. | 交流电源的周期必须等于粒子在D形盒中运动周期 |
17. 发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后经点火加速使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1与2相切于Q点,轨道2与3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后经点火加速使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1与2相切于Q点,轨道2与3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
 发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后经点火加速使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1与2相切于Q点,轨道2与3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )
发射地球同步卫星时,先将卫星发射到近地圆轨道1,然后经点火加速使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步圆轨道3.轨道1与2相切于Q点,轨道2与3相切于P点,如图所示,则当卫星分别在1、2、3轨道上正常运行时,以下说法正确的是( )| A. | 卫星在轨道3上的速率大于它在轨道1上的速率 | |
| B. | 卫星在轨道3上的角速度小于它在轨道1上的角速度 | |
| C. | 卫星在轨道1上经过Q点时的加速度小于它在轨道2上经 过Q 点时的加速度 | |
| D. | 卫星在轨道1上运动周期小于它在轨道3上运动周期 |
7.关于电场力和电场强度,下列说法中正确的是( )
| A. | 同一点电荷分别处于电场中的A、B两点,电荷受到的电场力大则该处场强大 | |
| B. | 电场中某点场强为零,则检验电荷在该点受到的电场力为零 | |
| C. | 在电场某点如果没有检验电荷,则电场力为零,电场强度也为零 | |
| D. | 一检验电荷在以一个点电荷为球心、半径为r的球面上各点所受电场力相同 |
14.下列说法正确的是( )
| A. | 当正电荷在电场中顺着电场线运动时,电荷的电势能增加 | |
| B. | 当负电荷在电场中逆着电场线运动时,电荷的电势能增加 | |
| C. | 当电荷在电场中移动时,电势能的改变量与零电势能点的选择无关 | |
| D. | 电荷在电场中的电势能与零势能点的选择无关 |
11.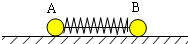 有两个质量不等的物体A、B,静止在光滑的水平面上,它们用细线连着,之间夹着一个被压缩的弹簧.当烧断细线,在弹簧恢复到原长的过程中( )
有两个质量不等的物体A、B,静止在光滑的水平面上,它们用细线连着,之间夹着一个被压缩的弹簧.当烧断细线,在弹簧恢复到原长的过程中( )
 有两个质量不等的物体A、B,静止在光滑的水平面上,它们用细线连着,之间夹着一个被压缩的弹簧.当烧断细线,在弹簧恢复到原长的过程中( )
有两个质量不等的物体A、B,静止在光滑的水平面上,它们用细线连着,之间夹着一个被压缩的弹簧.当烧断细线,在弹簧恢复到原长的过程中( )| A. | 弹簧对两个物体所做的功大小相等 | |
| B. | 弹簧和两个小球组成的系统机械能守恒 | |
| C. | 任何时刻两个物体加速度的大小都相等 | |
| D. | 任何时刻两个物体速度的大小都相等 |
12.力对物体做功的功率,下列说法正确的是( )
| A. | 功率是表示做功快慢的物理量,而不是表示做功大小的物理量 | |
| B. | 力对物体做功的时间越短,这个力的功率就越大 | |
| C. | 力对物体做的功越大,这个力的功率就一定越大 | |
| D. | 力对物体做功少,其功率就小,力对物体做功功多,其功率就大 |
 如图所示为平行板电容器,两极板间的电压为3V,现使它的电荷量减少3×10-4C,电容器两板间的电压减为原来的$\frac{1}{3}$,如果一个带正电微粒的质量m=$\sqrt{3}$×10-20kg,带电荷量q=1.0×10-20C,从电容器中的A点沿AB方向运动,已知AB和水平方向的夹角θ=30°,A,B相距L=20cm,微粒能够沿直线AB运动,则(取g=10m/s2)
如图所示为平行板电容器,两极板间的电压为3V,现使它的电荷量减少3×10-4C,电容器两板间的电压减为原来的$\frac{1}{3}$,如果一个带正电微粒的质量m=$\sqrt{3}$×10-20kg,带电荷量q=1.0×10-20C,从电容器中的A点沿AB方向运动,已知AB和水平方向的夹角θ=30°,A,B相距L=20cm,微粒能够沿直线AB运动,则(取g=10m/s2)