题目内容
10. 如图所示为平行板电容器,两极板间的电压为3V,现使它的电荷量减少3×10-4C,电容器两板间的电压减为原来的$\frac{1}{3}$,如果一个带正电微粒的质量m=$\sqrt{3}$×10-20kg,带电荷量q=1.0×10-20C,从电容器中的A点沿AB方向运动,已知AB和水平方向的夹角θ=30°,A,B相距L=20cm,微粒能够沿直线AB运动,则(取g=10m/s2)
如图所示为平行板电容器,两极板间的电压为3V,现使它的电荷量减少3×10-4C,电容器两板间的电压减为原来的$\frac{1}{3}$,如果一个带正电微粒的质量m=$\sqrt{3}$×10-20kg,带电荷量q=1.0×10-20C,从电容器中的A点沿AB方向运动,已知AB和水平方向的夹角θ=30°,A,B相距L=20cm,微粒能够沿直线AB运动,则(取g=10m/s2)(1)电容器的电容是多少?
(2)电场强度的大小和方向如何?
(3)要使微粒从A点运动到B点,微粒在A点时的最小速度是多少?
分析 (1)由电容的定义式即可求出电容器的电容;
(2)带电微粒做直线运动,所受的合力与速度在同一直线上,可以判断微粒的运动性质;然后由力的合成,求出电场强度的大小和方向;
(3)微粒从A点运动到B点,做匀减速运动,刚好到B点速度为零,由运动学公式求解微粒射入电场时的最小速度.
解答 解:(1)电容器的电荷量减少3×10-4C,电容器两板间的电压减为原来的$\frac{1}{3}$,即1V,极板之间的电压的变化为:△U=U0-U′=3-1=2V
所以的电容器的电容:C=$\frac{△Q}{△U}=\frac{3×1{0}^{-4}}{2}=1.5×1{0}^{-4}$F
(2)带电微粒做直线运动,所受的合力与速度在同一直线上.由于重力的方向竖直向下,所以电场力的方向必定是向左,正电荷受到的电场力的方向向左,所以场强的方向向左;由受力图可知:$tan30°=\frac{mg}{qE}$
所以:E=$\frac{\sqrt{3}mg}{q}$=30V/m
(3)点电荷受到的合力:ma=$\frac{mg}{sin30°}=2mg$
A到B做减速运动,则到达B的速度为0时,电荷在A点的速度最小,由运动学的公式得:
$0-{v}_{A}^{2}=-2a•\overline{AB}$
所以:${v}_{A}=2\sqrt{2}$m/s
答:(1)电容器的电容是1.5×10-4F;
(2)电场强度的大小是30V/m,方向水平向左;
(3)要使微粒从A点运动到B点,微粒在A点时的最小速度是$2\sqrt{2}$m/s.
点评 本题要掌握质点做直线运动的条件:合力与速度共线,由动能定理求解最小速度,也可以由牛顿第二定律和运动学公式结合进行研究.

练习册系列答案
相关题目
1.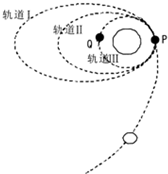 如图所示,嫦娥二号卫星进入地月转移轨道后,需经多次变轨才能最终进入距离月球表面100公里,周期为118分钟的工作轨道.下列有关嫦娥二号运动过程中说法正确的是( )
如图所示,嫦娥二号卫星进入地月转移轨道后,需经多次变轨才能最终进入距离月球表面100公里,周期为118分钟的工作轨道.下列有关嫦娥二号运动过程中说法正确的是( )
 如图所示,嫦娥二号卫星进入地月转移轨道后,需经多次变轨才能最终进入距离月球表面100公里,周期为118分钟的工作轨道.下列有关嫦娥二号运动过程中说法正确的是( )
如图所示,嫦娥二号卫星进入地月转移轨道后,需经多次变轨才能最终进入距离月球表面100公里,周期为118分钟的工作轨道.下列有关嫦娥二号运动过程中说法正确的是( )| A. | 由轨道Ⅰ转移到轨道Ⅱ时在P点要加速 | |
| B. | 在轨道Ⅰ上的最大速度比在轨道Ⅱ上的最大速度大 | |
| C. | 在轨道Ⅲ上经过P点的向心加速度比在轨道Ⅰ上经过P点时小 | |
| D. | 在轨道Ⅲ的运动速度比月球的第一宇宙速度大 |
1.物体由静止开始做匀加速直线运动,第7s内初速度是2.6m/s,则物体加速度是( )
| A. | 0.4m/s2 | B. | 0.37m/s2 | C. | 2.6m/s2 | D. | 0.43m/s2 |
18.下列叙述中,符合历史事实的是( )
| A. | 汤姆生通过对阴极射线的研究发现了电子 | |
| B. | 卢瑟福通过对α粒子散射实验的研究发现了质子 | |
| C. | 贝克勒尔通过对天然放射现象的研究发现了原子的核式结构 | |
| D. | 查德威克发现了中子并测出了中子的质量 |
5.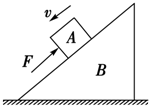 如图所示,一质量为M的斜面体B放在水平面上,在其斜面上放一质量为m的物体A,用一沿斜面向上的力F作用于物体A上,使其沿斜面匀速下滑,在物体A下滑的过程中,斜面体B静止不动,则地面对斜面体B的摩擦力Ff及支持力FN是( )
如图所示,一质量为M的斜面体B放在水平面上,在其斜面上放一质量为m的物体A,用一沿斜面向上的力F作用于物体A上,使其沿斜面匀速下滑,在物体A下滑的过程中,斜面体B静止不动,则地面对斜面体B的摩擦力Ff及支持力FN是( )
 如图所示,一质量为M的斜面体B放在水平面上,在其斜面上放一质量为m的物体A,用一沿斜面向上的力F作用于物体A上,使其沿斜面匀速下滑,在物体A下滑的过程中,斜面体B静止不动,则地面对斜面体B的摩擦力Ff及支持力FN是( )
如图所示,一质量为M的斜面体B放在水平面上,在其斜面上放一质量为m的物体A,用一沿斜面向上的力F作用于物体A上,使其沿斜面匀速下滑,在物体A下滑的过程中,斜面体B静止不动,则地面对斜面体B的摩擦力Ff及支持力FN是( )| A. | Ff=0,FN=Mg+mg | B. | Ff向左,FN<Mg+mg | C. | Ff向右,FN<Mg+mg | D. | Ff向左,FN=Mg+mg |
15. 质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点,如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时,木架停止转动,则( )
质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点,如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时,木架停止转动,则( )
 质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点,如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时,木架停止转动,则( )
质量为m的小球由轻绳a和b分别系于一轻质木架上的A点和C点,如图所示,当轻杆绕轴BC以角速度ω匀速转动时,小球在水平面内做匀速圆周运动,绳a在竖直方向,绳b在水平方向,当小球运动到图示位置时,绳b被烧断的同时,木架停止转动,则( )| A. | 小球仍在水平面内做匀速圆周运动 | |
| B. | 在绳b被烧断瞬间,a绳中张力突然增大 | |
| C. | 在绳b被烧断瞬间,小球的向心加速度不变 | |
| D. | 若角速度ω较大,小球可能在垂直于平面ABC的竖直平面内做圆周运动 |
20.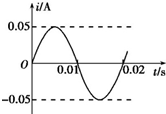 用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
 用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )
用220V的正弦交流电通过理想变压器对一负载供电,变压器输出电压是110V,通过负载的电流图象如图所示,则( )| A. | 变压器输入功率约为7.9W | |
| B. | 输出电压的最大值是110V | |
| C. | 变压器原、副线圈匝数比是1:2 | |
| D. | 负载电流的函数表达式i=0.05 sin (100πt)A |