��Ŀ����
4����һ��X���ǣ�������Զ��Ϊ��̽������ǣ�������һ���Ƹ�������Բ�˶������ǣ�������ƽ��������ϵĹ۲�վ��ͬһƽ���ڣ������ǵ������ת�����ڵ����ϵĹ۲�վ���֣��ٸ����ǵ���������Ϊv����t0ʱ���ڿɹ۲����Լt0ʱ���ڲ��ɼ�����1����X���ǵ�����M�Ƕ��٣�
��2�������������������ٶ�g���
��3���ڸ߶Ȳ�̫��ʱ�������ߣ�����������ڸ������������ʱ�����ܴ����������ٶ�ƽ�������ȣ�F=kv2�����������Ƿ���һ����ɴ����ͷŵĵ�½��������Ϊm����ͣ�ھ���������h��h��ʮ�ߣ�ԶС��X���ǵİ뾶�������õ�½�����Լ��ٶȵ��ڸ����������������ٶ�g�ȼ�������$\frac{h}{2}$��Ȼ������������������������ʹ֮�ȼ������䣬�ŵ��ٶ�ǡ��Ϊ�㣬�������Ե�½�������Ĺ�W����½�����������䵽�ŵص�ʱ��t��
���� ��1����������ó����ڣ��������ٶȹ�ʽ����뾶���������������ṩ��������
��2������������������������ʽ����������ٶȣ�
��3�������ȱ���ֱ���˶�λ��ʱ�乫ʽ��������ʱ�䣬�����ٶȹ�ʽ�������$\frac{h}{2}$���ٶȣ���������f=kv2���������ȼ����˶���������λ�������Թ�ϵ��������v2-x��f-x��ͼ���������̿˷������Ĺ�����f-xͼ���е�������ٽ�϶��ܶ�����ʽ��⼴�ɣ�
��� �⣺��1��������ã�T=2t0
���ٶ�v=$\frac{2��R}{T}$��
��ã�R=$\frac{v{t}_{0}}{��}$
�������������ṩ�������ã�$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$
��ã�M=$\frac{{v}^{2}R}{G}=\frac{{v}^{3}{t}_{0}}{��G}$
��2������$\frac{GMm}{{R}^{2}}=mg$
��ã�g=$\frac{GM}{{R}^{2}}=\frac{��v}{{t}_{0}}$
��3����½�����Լ��ٶȵ��ڸ����������������ٶ�g�ȼ�������$\frac{h}{2}$�����У�
$\frac{1}{2}h=\frac{1}{2}g{{t}_{1}}^{2}$
��ã�${t}_{1}=\sqrt{\frac{h}{g}}$��
��ʱ���ٶ�Ϊ��${v}_{1}=g{t}_{1}=\sqrt{\frac{��vh}{{t}_{0}}}$
���������䵽�ŵص�ʱ��Ϊ��t=2${t}_{1}=2\sqrt{\frac{h{t}_{0}}{��v}}$
��Ϊ��������f=kv2���������ȼ����˶���������${v}^{2}-{{v}_{0}}^{2}=2ax$��֪��
������λ�������Թ�ϵ����ͼ��v2-x��f-x����ͼ��ʾ��
�����������̿˷������Ĺ�����f-xͼ���е���������У�${W}_{f}=\frac{1}{2}k{{v}_{1}}^{2}h=\frac{��kv{h}^{2}}{2{t}_{0}}$
�跢�������Ĺ�ΪW�����ݶ��ܶ����ã�mgh-Wf+W=0
��ã�$W=\frac{��hv}{{t}_{0}}��\frac{kh}{2}-m��$
�𣺣�1����X���ǵ�����MΪ$\frac{{v}^{3}{t}_{0}}{��G}$��
��2�������������������ٶ�gΪ$\frac{��v}{{t}_{0}}$��
��3���������Ե�½�������Ĺ�WΪ$\frac{��hv}{{t}_{0}}��\frac{kh}{2}-m��$����½�����������䵽�ŵص�ʱ��tΪ$2\sqrt{\frac{h{t}_{0}}{��v}}$��
���� ������Ҫ���������������ṩ��������ʽ���˶�ѧ������ʽ�Լ����ܶ�����ֱ��Ӧ�ã�֪�����������������������������������Ҫ��ͬѧ���ܻ�����v2-x��f-x��ͼ����������̿˷������Ĺ�����f-xͼ���е������⣬�ѶȽϴ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | F=4F�� | B�� | F��=4F | C�� | F=F�� | D�� | F=16F�� |
 ��ͼ��ʾ�����һ�˹̶�����Ϊm��С������һ��0ΪԲ�ģ�ʹС�����뾶ΪR��Բ���˶�����С�����ߵ�ʱ��������
��ͼ��ʾ�����һ�˹̶�����Ϊm��С������һ��0ΪԲ�ģ�ʹС�����뾶ΪR��Բ���˶�����С�����ߵ�ʱ��������| A�� | �˶���ĵ��������ܵ����� | |
| B�� | С�����С�ٶ�Ϊ$\sqrt{gR}$ | |
| C�� | �˶����������һ��������������������ͬ | |
| D�� | �˶����������������������������෴ |
 ��ͼ��ʾ��a��b�������ɴ�����ͬ������ɣ�λ�ù̶���OΪab���е㣬O1 O2ͨ��O����ab��ֱ��һ�����ӣ������ɺ��ԣ���O2һ����O2O1�������룬����Ӵ���O�������˶��Ĺ����У�������
��ͼ��ʾ��a��b�������ɴ�����ͬ������ɣ�λ�ù̶���OΪab���е㣬O1 O2ͨ��O����ab��ֱ��һ�����ӣ������ɺ��ԣ���O2һ����O2O1�������룬����Ӵ���O�������˶��Ĺ����У�������| A�� | ���ĵ�������� | |
| B�� | ���ĵ�������С | |
| C�� | ���ļ��ٶȿ�ʼһ���Ӵ�����С | |
| D�� | ���ļ��ٶȿ�ʼһ����С������������ |
| A�� | VA��VB | B�� | VA��VB | C�� | tA��tB | D�� | tA��tB |
 ��һ�ο�����ֹ����У�һ��ֱ����A�ó�H=50m�������������ɺ��Բ��ƣ�ϵסһ����m=50kg�ı�����ԱB��ֱ����A�ͱ�����ԱB��v0=10m/s���ٶ�һ����ˮƽ���������˶�����ͼ����ʾ��ijʱ�̿�ʼ���������˵�����5sʱ���ڣ�A��B֮�����ֱ������l=50-t2����λ��m���Ĺ��ɱ仯��ȡg=10m/s2����
��һ�ο�����ֹ����У�һ��ֱ����A�ó�H=50m�������������ɺ��Բ��ƣ�ϵסһ����m=50kg�ı�����ԱB��ֱ����A�ͱ�����ԱB��v0=10m/s���ٶ�һ����ˮƽ���������˶�����ͼ����ʾ��ijʱ�̿�ʼ���������˵�����5sʱ���ڣ�A��B֮�����ֱ������l=50-t2����λ��m���Ĺ��ɱ仯��ȡg=10m/s2����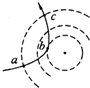 ���ݦ�����ɢ��ʵ�飬¬ɪ�������ԭ�ӵĺ�ʽ�ṹģ�ͣ���ͼ�����߱�ʾԭ�Ӻ����γɵĵ糡�ĵ����ߣ�ʵ�߱�ʾһ�������ӵ��˶��켣���ڦ����Ӵ�a�˶���b�����˶���c�Ĺ����У������ӵĶ����ȼ�С��������������������С�����������С�����䡱��
���ݦ�����ɢ��ʵ�飬¬ɪ�������ԭ�ӵĺ�ʽ�ṹģ�ͣ���ͼ�����߱�ʾԭ�Ӻ����γɵĵ糡�ĵ����ߣ�ʵ�߱�ʾһ�������ӵ��˶��켣���ڦ����Ӵ�a�˶���b�����˶���c�Ĺ����У������ӵĶ����ȼ�С��������������������С�����������С�����䡱��
