题目内容
(12分)如图所示,光滑水平面上有一块木板,质量M=2.0 kg,长度L=1.0m。在木板的最右端有一个小滑块(可视为质点),质量m=1.0 kg。小滑块与木板之间的动摩擦因数μ=0.2。开始时它们都处于静止状态。某时刻起对小滑块施加一个F="5.0" N水平向左的恒力,此后小滑块将相对木板滑动。取g ="10" m/s2。求:
(1)小滑块从木板右端运动到左端所用的时间t;
(2)小滑块从木板右端运动到左端的过程中,恒力F对小滑块所做的功W;
(3)如果想缩短小滑块从木板右端运动到左端所用的时间t,只改变木板的质量M,请你通过计算,判断木板的质量M应该增大还是减小?
(1)1.0s (2) 7.5J (3) M增加时,t减小
解析试题分析:小滑块受到水平向左的恒力F和水平向右的滑动摩擦力作用,向左做匀加速直线运动,所受滑动摩擦力 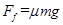 =" 0.2×1.0×10" =" 2.0(N)"
=" 0.2×1.0×10" =" 2.0(N)"
根据牛顿第二定律,小滑块的加速度 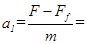 3.0 (m/s2)
3.0 (m/s2)
木板所受向左的滑动摩擦力 ,向左做匀加速直线运动。
,向左做匀加速直线运动。
根据牛顿第二定律,木板的加速度 =1.0(m/s2)
=1.0(m/s2)
在小滑块从木板右端运动到左端所用的时间为t内,小滑块的位移
木板的位移
由几何关系可知L= x1 – x2 
解得 t =" 1.0" (s)
(2) 小滑块的位移 ="1.5" (m)
="1.5" (m)
恒力F对小滑块所做的功 W = Fx1 =" 5.0×1.5" =" 7.5" (J)
(3)由于x1 – x2= L,即
将(1)中各式代入,有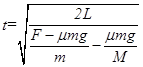 ,若只改变M,则M增加时,t减小。
,若只改变M,则M增加时,t减小。
考点:牛顿运动定律、相对运动、恒力做功

如图所示,一小球从A点由静止开始沿斜面向下做匀变速直线运动,若到达B点时速度为v,到达C点时速度为2v,则xAB∶xBC等于 ( )
| A.1∶1 | B.1∶2 | C.1∶3 | D.1∶4 |
2012年6月1日.空降兵某部官兵使用新装备从260米超低空跳伞成功。如图所示,若跳伞空降兵在离地面224m高处.由静止开始在竖直方向做自由落体运动。—段时间后.立即打开降落伞,以12.5m/s2的平均加速度匀减速下降.为了空降兵的安全,要求空降兵落地速度最大不得超过5m/s(g取10m/s2)。则
| A.空降兵展开伞时离地面高度至少为125m,相当于从2.5m高处自由落下 |
| B.空降兵展开伞时离地面高度至少为125m,相当于从1.25m高处自由落下 |
| C.空降兵展开伞时离地面髙度至少为99m,相当于从1.25m高处自由落下 |
| D.空降兵展开伞时离地面高度至少为99m ,相当于从2.5m高处自由落下 |
近年来,我国通过改造原有铁路线路(直线化、轨距标准化) ,使列车营运速率达到每小时200公里以上,这类高速铁路简称“高铁”。假设列车在某段距离中做匀加速直线运动,速度由零增加到v时位移为x。当速度由v增加到2v时,其位移为
| A.x | B.2x | C.3x | D.4x |
汽车正在以 10m/s的速度在平直的公路上匀速前进,在它的正前方x处有一辆自行车以 4m/s的速度做同方向的匀速直线运动,汽车立即关闭油门做a =" -" 6m/s2的匀变速运动,若汽车恰好碰不上自行车,则x的大小为 ( )
| A.9.67m | B.3.33m | C.3m | D.7m |
如图所示,长度L="10" m的水平传送带以速率v0="4" m/s沿顺时针方向运行,质量m="1" kg的小物块(可视为质点)以v1="6" m/s的初速度从右端滑上传送带。已知物块与传送带之间的动摩擦因数μ=0.4,重力加速度g="10" m/s2,则物块:AD
| A.相对地面向左运动的最大距离为4.5m |
| B.相对地面向左运动的最大距离为10.5m |
| C.从滑上传送带到滑下传送带所用的时间2.5 s |
| D.从滑上传送带到滑下传送带所用的时间3.125 s |
如图所示,t=0时,质量为m= lkg的物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点。现将不同时刻的瞬时速度记录在下表中,由此可知( )(g=10m/s2)

| A.物体运动过程中的最大速度为12m/s |
| B.t=4s时刻物体恰好经过B点 |
| C.t=15s时刻物体恰好停在C点 |
| D.AB间距离小于BC间距离 |
一辆汽车从静止开始匀加速运动,下表给出了某些时刻汽车的瞬时速度,根据表中的数据通过分析、计算可以得出( )
| 时刻(s) | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 速度(m/s) | 3.0 | 6.0 | 9.0 | 12 | 15 | 18 |
B.汽车前6 s内的位移为36 m
C.汽车第8 s的速度为24 m/s
D.汽车运动第7 s内的位移为16 m