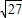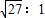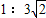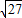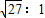题目内容
有两颗人造地球卫星绕地球做匀速圆周运动,设两颗人造地球卫星的质量之比为1:2,轨道半径之比为3:1,则下列比值正确的是( )
分析:人造地球卫星的向心力由万有引力提供,则由公式可得出各量的表达式,则可得出各量间的比值.
解答:解:人造地球卫星的万有引力充当向心力,即
=ma=m
=mrω2=m
,则可知:
A、线速度v=
,故线速度之比为:1:
,故A错误;
B、周期T=2π
,故周期之比为
:1,故B正确;
C、向心加速度a=
,故向心加速度为1:9,故C正确;
D、角速度ω=
,故角速度之比为1:
,故D错误;
故选BC.
| GMm |
| r2 |
| v2 |
| r |
| 4π2r |
| T2 |
A、线速度v=
|
| 3 |
B、周期T=2π
|
| 27 |
C、向心加速度a=
| GM |
| r2 |
D、角速度ω=
|
| 27 |
故选BC.
点评:本题考查万有引力在天体运动中的应用,注意本题中的质量为中心天体地球的质量;各物理量与人造地球卫星的质量无关.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
有两颗人造地球卫星绕地球做匀速圆周运动,设两颗人造地球卫星的质量之比为1:2,轨道半径之比为4:1,则下列比值正确的是( )
| A、这两颗卫星的线速度之比是1:8 | B、这两颗卫星的周期之比是8:1 | C、这两颗卫星的向心加速度之比是1:16 | D、这两颗卫星的角速度之比是1:16 |