Question

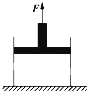
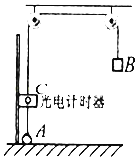
【题目】某同学利用图示的装置来验证机械能守恒定律．设计了如下实验，A是质量为m、直径为d的小球，B为重物，AB间用轻质细绳通过轻质滑轮相连．在距水平地面h高处的C点固定一个光电计时器．实验操作如下：

①开始时，测出重物B的质量M，将小球A放在光电计时器正下方的水平地面上，系统在外力作用下保持静止．细绳拉直但张力为零，现释放B使其向下运动．测出小球A通过光电计时器所用的时间为△t，且小球A 通过光电计时器时重物B还未落地

②实验中保持A质量不变，改变B的质量，多次重复笫（1）步

（1）实验中，M和m的关系必须满足M_____m（选填“小于”、“等于”或“大于”）

（2）小球A运动至C点的速度可表示为_____．

（3）根椐所测数据，为得到线性关系图线，应作出_____（选填“△t﹣”“△t2﹣”或“△t2﹣”）图线；

（4）根据第（3）问得到的图线，若图线在纵轴上的截距为b，则当地重力加速度g=_____（用题给的己知量表示）

Answer 1

【答案】 （1）大于 （2） （3）△t2﹣ （4）

【解析】解：（1）释放B后小球要向上运动，A所受合力应向上，因此B的质量M应大于A的质量m．

（2）小球经过光电门时的速度：v=；

（3）对系统，由机械能守恒定律得：（M﹣m）gh=（M+m）v2，

整理得：△t2=，△t2与是线性关系，为得出线性关系图线，应作：△t2﹣图象；

（4）△t2﹣图象的截距：b=，解得：g=；