题目内容
13. 如图1所示,一边长为10cm的实心立方体木块,一只昆虫从A点爬列G点.求:
如图1所示,一边长为10cm的实心立方体木块,一只昆虫从A点爬列G点.求:(1)该昆虫的位移;
(2)该昆虫的最短路程.
分析 位移是初位置指向末位置的有向线段,从相邻的两个面到达G才可能最短,我们可以把面AEFD和面CDFG展开,根据几何关系求解.
解答  解:(1)昆虫只能沿木块表面从A点到G点,位移为立方体对角线的长度x=$\sqrt{1{0}^{2}+(10\sqrt{2})^{2}}=10\sqrt{3}cm$,
解:(1)昆虫只能沿木块表面从A点到G点,位移为立方体对角线的长度x=$\sqrt{1{0}^{2}+(10\sqrt{2})^{2}}=10\sqrt{3}cm$,
(2)其最短路程分析可知:应该从相邻的两个面到达G才可能最短,我们可以把面AEFD和面CDFG展开,如图,
连接A与G,AIG的长度就是最短路程s=$\sqrt{1{0}^{2}+2{0}^{2}}=10\sqrt{5}$cm,
答:(1)该昆虫的位移为$10\sqrt{3}cm$;
(2)该昆虫的最短路程为$10\sqrt{5}cm$.
点评 本题主要考查了路程和位移的区别与联系,知道位移是初位置指向末位置的有向线段,路程是运动轨迹的长度.

练习册系列答案
相关题目
3. 如图所示,长L的轻杆一端固定一个质量为m的小球,另一端固定在光滑水平转动轴O上,杆可以在竖直面内绕轴转动.已知小球通过最低点Q时的速度大小为2$\sqrt{gL}$,则下列说法中正确的( )
如图所示,长L的轻杆一端固定一个质量为m的小球,另一端固定在光滑水平转动轴O上,杆可以在竖直面内绕轴转动.已知小球通过最低点Q时的速度大小为2$\sqrt{gL}$,则下列说法中正确的( )
 如图所示,长L的轻杆一端固定一个质量为m的小球,另一端固定在光滑水平转动轴O上,杆可以在竖直面内绕轴转动.已知小球通过最低点Q时的速度大小为2$\sqrt{gL}$,则下列说法中正确的( )
如图所示,长L的轻杆一端固定一个质量为m的小球,另一端固定在光滑水平转动轴O上,杆可以在竖直面内绕轴转动.已知小球通过最低点Q时的速度大小为2$\sqrt{gL}$,则下列说法中正确的( )| A. | 小球能达到圆周轨道的最高点P,且在P点受到杆对它向上的弹力 | |
| B. | 小球能达到圆周轨道的最高点P,且在P点受到杆对它向下的弹力 | |
| C. | 小球能达到圆周轨道的最高点P,且在P点不受杆对它的弹力 | |
| D. | 小球不可能达到圆周轨道的最高点P |
4.某物体的位移-时间图象如图所示,则下列叙述正确的是( )


| A. | 物体运动的轨迹是抛物线 | |
| B. | 物体运动所能达到的最大位移为80 m | |
| C. | 物体先做加速运动,后做减速运动 | |
| D. | 在t=4 s时刻,物体的瞬时速度为零 |
18. 乘坐游乐场的过山车时,质量为m的人随车在竖直平面内沿圆轨道运动,如图所示,下列说法正确的是( )
乘坐游乐场的过山车时,质量为m的人随车在竖直平面内沿圆轨道运动,如图所示,下列说法正确的是( )
 乘坐游乐场的过山车时,质量为m的人随车在竖直平面内沿圆轨道运动,如图所示,下列说法正确的是( )
乘坐游乐场的过山车时,质量为m的人随车在竖直平面内沿圆轨道运动,如图所示,下列说法正确的是( )| A. | 车在最高点时,人处于倒坐状态,全靠保险带拉住,若没有保险带,人一定会掉下来 | |
| B. | 人在最低点时,对座位的压力大于mg | |
| C. | 人在最高点时,对座位仍可能产生压力,但压力一定小于mg | |
| D. | 人在最低点时,处于超重状态 |
2.物理学家勇于创新、实事求是的科学态度、科学思想和方法,始终激励着我们.以下说法符合物理史实的是( )
| A. | 亚里士多德发现了力是改变物体运动状态的原因 | |
| B. | 伽利略认为在同一地点,重的物体和轻的物体下落快慢不同 | |
| C. | 伽利略根据理想斜面实验,提出力不是维持物体运动状态的原因 | |
| D. | 开普勒对第谷观测的行星数据进行多年研究,得出了万有引力定律 |
3.下列计时数据指的是时刻的是( )
| A. | 在整个90分钟的比赛中,甲、乙两足球队“互交白卷” | |
| B. | 他每天都看电视节目“新闻早8点” | |
| C. | 列车到站时间晚点5分钟 | |
| D. | 高考数学考试的时间是2小时 |
 如图所示,质量m=10kg的重物,在方向竖直向上的拉力作用下,由静止开始匀速上升,加速度为5m/s2,上升10米,不计空气阻力,g取10m/s2.求:
如图所示,质量m=10kg的重物,在方向竖直向上的拉力作用下,由静止开始匀速上升,加速度为5m/s2,上升10米,不计空气阻力,g取10m/s2.求: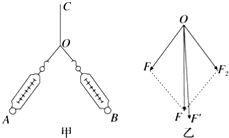 在“验证力的平行四边形定则”的实验中,某小组利用如图甲所示的装置完成实验,橡皮条的一端C固定在木板上,用两只弹簧测力计把橡皮条的另一端拉到某一确定的O点.
在“验证力的平行四边形定则”的实验中,某小组利用如图甲所示的装置完成实验,橡皮条的一端C固定在木板上,用两只弹簧测力计把橡皮条的另一端拉到某一确定的O点.