题目内容
 如图所示,轻质弹簧将质量为m的小物块连接在质量为M(M=3m)的光滑框架内.小物块位于框架中心位置时弹簧处于自由长度.现框架与小物块共同以速度V沿光滑水平面向左匀速滑动.
如图所示,轻质弹簧将质量为m的小物块连接在质量为M(M=3m)的光滑框架内.小物块位于框架中心位置时弹簧处于自由长度.现框架与小物块共同以速度V沿光滑水平面向左匀速滑动.(1)若框架与墙壁发生瞬间碰撞后速度为0且与墙壁间不粘连,求框架刚要脱离墙壁时小物块速度的大小和方向;
(2)在(1)情形下,框架脱离墙壁后的运动过程中,弹簧弹性势能的最大值
(3)若框架与墙壁发生瞬间碰撞,立即反弹,在以后过程中弹簧的最大弹性势能为2/3mvo2,求框架与墙壁碰撞时损失的机械能△E1
(4)在(3)情形下试判定框架与墙壁能否发生第二次碰撞?若不能,说明理由.若能,试求出第二次碰撞时损失的机械能△E2.(设框架与墙壁每次碰撞前后速度大小之比不变)
【答案】分析:(1)框架与墙壁碰撞后,物块以v压缩弹簧,后又返回,由机械能守恒可知,碰后速度仍为v方向向右.
(2)设弹簧有最大势能时共同速度为v,根据动量守恒定律和能量守恒定律列式即可求解;
(3)设框架反弹速度为v1、最大势能时共同速度为v,则由动量、能量守恒定律即可求解v1、和v,从而求解损失量;
(4)由(3)知第一次碰后反弹后,二者总动量为零,故当弹簧再次伸展后仍可继续与墙壁相撞,并以v1的速度与墙壁相撞,根据速度的比值关系求得碰后速度即可求解机械能损失量.
解答:解:(1)框架与墙壁碰撞后,物块以V压缩弹簧,后又返回,当返回原位时框架开始离开,由机械能守恒知,此时物块速度是v方向向右.
(2)设弹簧有最大势能时共同速度为v 由动量守恒定律知 mv=4mv
由能量守恒定律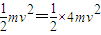 +EP×
+EP×
EP=
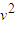
(3)设框架反弹速度为v1、最大势能时共同速度为v,则
由动量、能量守恒定律得
3mv1-mv=4mv
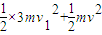 =
=
解得:9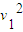 +18v1v-7
+18v1v-7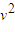 =0 v1=
=0 v1=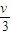
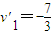 v(舍去)
v(舍去)
带入得:v=0
△E1=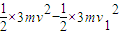 =
=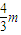
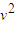
(4)由(3)知第一次碰后反弹后,二者总动量为零,故当弹簧再次伸展后仍可继续与墙壁相撞,并以V1=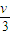 的速度与墙壁相撞,由题意知,
的速度与墙壁相撞,由题意知,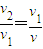 所以
所以 
故△E2=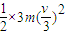 -
-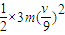 =
=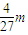
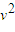
答:(1)若框架与墙壁发生瞬间碰撞后速度为0且与墙壁间不粘连,框架刚要脱离墙壁时小物块速度的大小为v,方向向右;
(2)在(1)情形下,框架脱离墙壁后的运动过程中,弹簧弹性势能的最大值为 mv2;
mv2;
(3)框架与墙壁碰撞时损失的机械能为 mv2;
mv2;
(4)能,第二次碰撞时损失的机械能为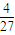 mv2.
mv2.
点评:本题主要考查了动量守恒定律和能量守恒定律的直接应用,要求同学们能正确分析物体的运动过程,难度适中.
(2)设弹簧有最大势能时共同速度为v,根据动量守恒定律和能量守恒定律列式即可求解;
(3)设框架反弹速度为v1、最大势能时共同速度为v,则由动量、能量守恒定律即可求解v1、和v,从而求解损失量;
(4)由(3)知第一次碰后反弹后,二者总动量为零,故当弹簧再次伸展后仍可继续与墙壁相撞,并以v1的速度与墙壁相撞,根据速度的比值关系求得碰后速度即可求解机械能损失量.
解答:解:(1)框架与墙壁碰撞后,物块以V压缩弹簧,后又返回,当返回原位时框架开始离开,由机械能守恒知,此时物块速度是v方向向右.
(2)设弹簧有最大势能时共同速度为v 由动量守恒定律知 mv=4mv
由能量守恒定律
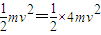 +EP×
+EP×EP=

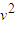
(3)设框架反弹速度为v1、最大势能时共同速度为v,则
由动量、能量守恒定律得
3mv1-mv=4mv
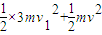 =
=
解得:9
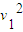 +18v1v-7
+18v1v-7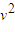 =0 v1=
=0 v1=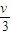
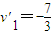 v(舍去)
v(舍去)带入得:v=0
△E1=
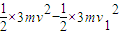 =
=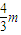
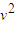
(4)由(3)知第一次碰后反弹后,二者总动量为零,故当弹簧再次伸展后仍可继续与墙壁相撞,并以V1=
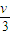 的速度与墙壁相撞,由题意知,
的速度与墙壁相撞,由题意知,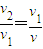 所以
所以 
故△E2=
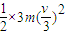 -
-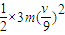 =
=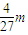
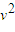
答:(1)若框架与墙壁发生瞬间碰撞后速度为0且与墙壁间不粘连,框架刚要脱离墙壁时小物块速度的大小为v,方向向右;
(2)在(1)情形下,框架脱离墙壁后的运动过程中,弹簧弹性势能的最大值为
 mv2;
mv2;(3)框架与墙壁碰撞时损失的机械能为
 mv2;
mv2;(4)能,第二次碰撞时损失的机械能为
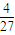 mv2.
mv2.点评:本题主要考查了动量守恒定律和能量守恒定律的直接应用,要求同学们能正确分析物体的运动过程,难度适中.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 如图所示,轻质弹簧将质量为m的小物块连接在质量为M(M=3m)的光滑框架内.小物块位于框架中心位置时弹簧处于自由长度.现框架与小物块共同以速度V0沿光滑水平面向左匀速滑动.
如图所示,轻质弹簧将质量为m的小物块连接在质量为M(M=3m)的光滑框架内.小物块位于框架中心位置时弹簧处于自由长度.现框架与小物块共同以速度V0沿光滑水平面向左匀速滑动. (2)若框架与墙壁发生瞬间碰撞,立即反弹,在以后过程中弹簧的最大弹性势能为
(2)若框架与墙壁发生瞬间碰撞,立即反弹,在以后过程中弹簧的最大弹性势能为
