题目内容
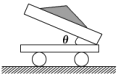
【题目】如图所示，质量足够大、截面是直角梯形的物块静置在光滑水平地面上，其两个侧面恰好与两个固定在地面上的压力传感器X和Y相接触。图中AB高H=0．3m，AD长L=0．5m，斜面倾角θ=37°。可视为质点的小物块P（图中未画出）质量m=1kg，它与斜面的动摩擦因数μ可以通过更换斜面表面的材料进行调节（调节范围是0≤μ≤1）。sin37°=0．6，cos37°=0．8，重力加速度g取l0m／s2。
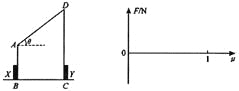
（1）令μ=0，将P由D点静止释放，求P在斜面上的运动时间；
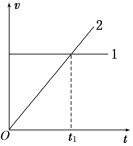
（2）将X和Y接到同一数据处理器上，已知当X和Y受到物块压力时，分别显示正值和负值。对于不同的μ，每次都在D点给P一个沿斜面向下足够大的初速度以保证它能滑离斜面，求滑行过程中处理器显示的读数F随μ变化的关系表达式，并在坐标系中画出其函数图象。
【答案】（1）
（2）
【解析】试题分析：（1）当
时．设P沿斜面下滑的加速度为a，P在斜面上运动的时间为t
由牛顿第二定律得： 
由运动学公式得： 
解得： 
（2）P沿斜面下滑的过程中，物块的受力如图所示，设传感器对物块的压力为F，取向右为正方向，由平衡条件可得：
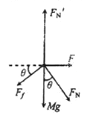
由P物体知： 
， 
，代入数据解得： 
其图象如图所示。
练习册系列答案
浙江名校名师金卷系列答案
相关题目
