题目内容
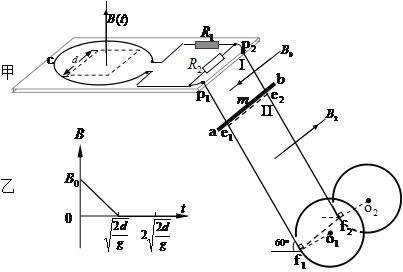
【题目】如图所示,平面直角坐标系石盼位于竖直平面内,M是一块平行于x轴的挡板,与y轴交点的坐标为(![]() ),右端无限接近虚线POQ上的N点,粒子若打在挡板上会被挡板吸收。虚线POQ与x轴正方向的夹角为60°,其右侧区域I内存在垂直纸面向外的匀强磁场,磁感应强度为B,挡板上方区域Ⅱ内存在垂直纸面向外的匀强磁场,磁感应强度为2B,挡板下方区域Ⅲ内存在方向沿x轴正方向的匀强电场。O点有两个质量均为m、电荷量分别为+q的粒子a和-q的粒子b,以及一不带电的粒子c.粒子重力不计,q>0。
),右端无限接近虚线POQ上的N点,粒子若打在挡板上会被挡板吸收。虚线POQ与x轴正方向的夹角为60°,其右侧区域I内存在垂直纸面向外的匀强磁场,磁感应强度为B,挡板上方区域Ⅱ内存在垂直纸面向外的匀强磁场,磁感应强度为2B,挡板下方区域Ⅲ内存在方向沿x轴正方向的匀强电场。O点有两个质量均为m、电荷量分别为+q的粒子a和-q的粒子b,以及一不带电的粒子c.粒子重力不计,q>0。

(1)若粒子a从O点以速率v0沿y轴正方向射入区域Ⅲ,且恰好经过N点,求场强大小E;
(2)若粒子b从O点沿x轴正方向射入区域I,且恰好经过N点,求粒子b的速率vb;
(3)若粒子b从O点以(2)问中速率沿x轴正方向射入区域I的同时,粒子c也从O点以速率vc沿OQ方向匀速运动,最终两粒子相遇,求vc的可能值。
【答案】(1)![]() (2)若粒子b由轨迹①到达N点,
(2)若粒子b由轨迹①到达N点,![]() ;若粒子b由轨迹②到达N点,
;若粒子b由轨迹②到达N点,![]() (3)i.若粒子b由轨迹①到达N1点和粒子c相遇,则
(3)i.若粒子b由轨迹①到达N1点和粒子c相遇,则![]() ;ii.若粒子b由轨迹②经区域Ⅱ到达各个交点和粒子c相遇,
;ii.若粒子b由轨迹②经区域Ⅱ到达各个交点和粒子c相遇,![]() ;iii.若粒子b由轨迹②经区域I到达各个交点和粒子c相遇,
;iii.若粒子b由轨迹②经区域I到达各个交点和粒子c相遇,![]()
【解析】
试题分析:(1)粒子a在电场中做类平抛运动
竖直方向上有![]()
水平方向上有![]()
又![]()
联立解得![]()
(2)如图甲所示:粒子b在磁场中做匀速圆周运动。
i.若粒子b由轨迹①到达N点,由几何知识有ON=2R1cos30°,ON=L
解得![]() R1
R1
根据洛伦兹力提供向心力,有![]()
解得![]()
ii.若粒子b由轨迹②到达N点,由![]() ,
,
得![]() ,
,![]() ,即
,即![]()
由几何知识有![]() ,
,![]() ,
,![]()
得![]() ,解得
,解得![]()
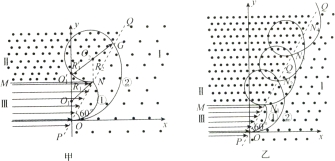
(3)如图乙所示,设粒子b每次经过虚线POQ时交点为N1、N2、N3、N4……
则相邻交点之间的距离均为![]() 根据粒子在磁场中运动周期
根据粒子在磁场中运动周期![]() ,
,
在区域I中每段圆弧对应的运动时间为![]()
在区域Ⅱ中每段圆弧对应的运动时间为![]()
故可设![]() ,
,
i.若粒子b由轨迹①到达N1点和粒子c相遇,则![]()
ii.若粒子b由轨迹②经区域Ⅱ到达各个交点和粒子c相遇,粒子c运动的位移大小为nL,对应的时间为2nt,![]()
iii.若粒子b由轨迹②经区域I到达各个交点和粒子c相遇,粒子c运动的位移大小为nL,对应的时间为(2n-3)t,
![]() [或
[或![]() ]
]

 计算高手系列答案
计算高手系列答案