题目内容
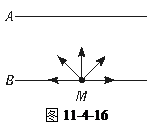 如图11-4-16所示,两块垂直纸面的平行金属板A、B相距d=10.0 cm,B板的中央M处有一个α粒子源,可向各个方向射出速率相同的α粒子,α粒子的比荷q/m=4.82×107 C/kg,为使所有α粒子都不能达到A板,可以在A、B板间加一个电压,所加电压最小值是U0=4.15×104 V;若撤去A、B间的电压,仍使所有α粒子都不能到达A板,可以在A、B间加一个垂直纸面的匀强磁场,该匀强磁场的磁感应强度B必须符合什么条件?
如图11-4-16所示,两块垂直纸面的平行金属板A、B相距d=10.0 cm,B板的中央M处有一个α粒子源,可向各个方向射出速率相同的α粒子,α粒子的比荷q/m=4.82×107 C/kg,为使所有α粒子都不能达到A板,可以在A、B板间加一个电压,所加电压最小值是U0=4.15×104 V;若撤去A、B间的电压,仍使所有α粒子都不能到达A板,可以在A、B间加一个垂直纸面的匀强磁场,该匀强磁场的磁感应强度B必须符合什么条件?
B≥0.83 T
解析:
设射出的α粒子速率为v,在电场力作用下最容易到达A板的是速度方向垂直B板的α粒子,因为所有α粒子在垂直极板方向分运动的加速度相同,而垂直极板射出的α粒子在这个方向的初速度最大,如果这个α粒子不能达到A板,则所有α粒子都不能到达A板.由动能定理得:qU0=![]() mv2 ,α粒子的速率为
mv2 ,α粒子的速率为![]() .
.
加磁场后,速率相同的α粒子做匀速圆周运动的轨道半径都相同,初速度方向沿B板的α粒子最容易到达A板,因为其过起点的直径垂直于极板.当α粒子的轨道半径不大于d/2,取轨迹与AB板都相切的α粒子,即轨道半径等于d/2的临界情况,与此对应的磁感应强度就是使所有α粒子都不能到达极板A的最小磁感应强度.
因为:Bqv=![]() 将上述速度代入可得:B=
将上述速度代入可得:B=![]() =
=![]() =0.83 T,
=0.83 T,
即磁感应强度应满足B≥0.83 T.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目




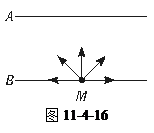 如图11-4-16所示,两块垂直纸面的平行金属板A、B相距d=10.0 cm,B板的中央M处有一个α粒子源,可向各个方向射出速率相同的α粒子,α粒子的比荷q/m=4.82×107 C/kg,为使所有α粒子都不能达到A板,可以在A、B板间加一个电压,所加电压最小值是U0=4.15×104 V;若撤去A、B间的电压,仍使所有α粒子都不能到达A板,可以在A、B间加一个垂直纸面的匀强磁场,该匀强磁场的磁感应强度B必须符合什么条件?
如图11-4-16所示,两块垂直纸面的平行金属板A、B相距d=10.0 cm,B板的中央M处有一个α粒子源,可向各个方向射出速率相同的α粒子,α粒子的比荷q/m=4.82×107 C/kg,为使所有α粒子都不能达到A板,可以在A、B板间加一个电压,所加电压最小值是U0=4.15×104 V;若撤去A、B间的电压,仍使所有α粒子都不能到达A板,可以在A、B间加一个垂直纸面的匀强磁场,该匀强磁场的磁感应强度B必须符合什么条件?