题目内容
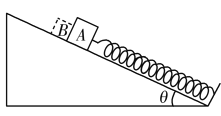
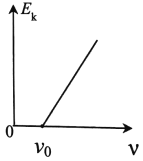
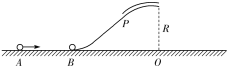
【题目】如图所示，倾斜轨道底端用一小段圆弧与水平面平滑连接，上端与半径为R=0.5 m的圆管形轨道相切于P点，圆管顶端开口水平，距离水平面的高度为R。质量为m=0.2 kg的小球B静止在斜面的底端。另有质量相同的小球A以初速度v0=5 m/s沿水平面向右运动，并与小球B发生弹性碰撞，不考虑一切摩擦，重力加速度g取10 m/s2。
(1)求小球B被碰后的速度大小；
(2)求小球B到达圆管形轨道最高点时对轨道的压力大小和方向；
(3)若保持小球A的初速度不变，增加其质量，则小球B从轨道的最高点抛出后，求小球B的落地点到O点的最远距离不会超过多少。
【答案】(1) 5 m/s (2) 向上的压力，大小为4 N (3) 不会超过3 m
【解析】
(1)设A、B两球碰撞后的速度分别为v1、v2，A、B两球发生弹性碰撞，由动量守恒定律得mv0=mv1＋mv2
由能量守恒定律得
联立解得v1=0、v2=v0=5 m/s
(2)A、B两小球碰撞后，设小球B沿轨道上升到最高点的速度为v，则有动能定理得
－mgR=
mv2－
在圆管形轨道的最高点，设轨道对小球的支持力为FN，由牛顿第二定律可得mg－FN=m
联立解得FN=－4 N
负号说明圆管形轨道对小球有向下的压力，根据牛顿第三定律可得，小球在最高点对轨道有向上的压力，大小为4 N
(3)设小球A的质量为M，则由动量守恒定律和能量守恒定律有Mv0=Mv3＋mv4
联立解得v4=
v0
当小球A的质量M无限增加时，碰撞后小球B的速度都不会超过2v0
设小球B到达轨道最高点的速度为v′，则有－mgR=mv′2－m(2v0)2
解得v′=3
m/s
由平抛运动的规律有R=gt2，xm=v′t
联立解得xm=3 m
所以小球B从轨道的最高点抛出后，落地点到O点的最远距离不会超过3 m
