题目内容
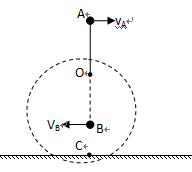
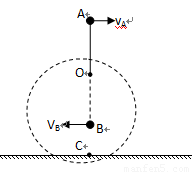
如图所示,一长为R的轻绳在左端系一质量为m的小球A、右端固定于O点,质量为M的木板B静止在光滑的水平面上,有一质量为m的滑块C(可视为质点)位于木板B左端O点的正下方.现将轻绳拉至水平,由静止释放小球A,小球A摆至最低点与滑块C发生弹性正碰,设木板足够长,求最终B、C一起运动的速度.

分析:小球A与C发生弹性正碰,遵守动量守恒和动能守恒,由两大守恒列式求出碰后C的速度.C获得速度后在木板B上向右滑动,C与B的系统动量守恒,最终两者一起做匀速直线运动,根据动量守恒定律求解共同速度.
解答:解:设A到达最低点与C碰撞前的速度大小为v.
A向下摆动过程,由机械能守恒定律得:mgR=
mv2
则得 v=
对于A、C碰撞过程,由动量守恒和动能守恒得:
mv=mvA+mvC
mv2=
m
+
m
解得,vC=v
C获得速度后在木板B上向右滑动,最终两者速度相同,设共同速度为v′,则根据动量守恒得
mvC=(m+M)v′
解得,v′=
答:最终B、C一起运动的速度为
.
A向下摆动过程,由机械能守恒定律得:mgR=
| 1 |
| 2 |
则得 v=
| 2gR |
对于A、C碰撞过程,由动量守恒和动能守恒得:
mv=mvA+mvC
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 A |
| 1 |
| 2 |
| v | 2 C |
解得,vC=v
C获得速度后在木板B上向右滑动,最终两者速度相同,设共同速度为v′,则根据动量守恒得
mvC=(m+M)v′
解得,v′=
| m |
| m+M |
| 2gR |
答:最终B、C一起运动的速度为
| m |
| m+M |
| 2gR |
点评:本题分析物体运动过程,把握每个过程遵守的物理规律是关键.对于A、C,由于质量相等,发生弹性碰撞后,交换速度,这个结论要理解记牢.

练习册系列答案
相关题目
 如图所示,一半径为r的球的质量为m,它被长为r的细绳挂在光滑的竖直墙壁上.则下列判断正确的是( )
如图所示,一半径为r的球的质量为m,它被长为r的细绳挂在光滑的竖直墙壁上.则下列判断正确的是( )