��Ŀ����
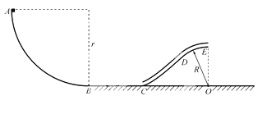
����Ŀ����ͼ��ʾ���㹻���Ĵ��ʹ���ˮƽ��������Ϊ�������aͨ��ƽ���ڴ��ʹ�����������⻬�Ử�������b������b������Ϊm����ʼʱ��a��b�����ʹ�����ֹ���ҿ�ʼʱaǡ����Ħ�������á����ô��ʹ�˳ʱ������ת��������b�½�h�߶�(aδ���봫�ʹ�)�Ĺ�����
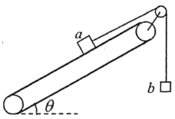
A. ���a�������������� mghsin��
B. Ħ������a���Ĺ�����a��bϵ����е�ܵ�����
C. ���ʹ���������a�����ĵĵ��ܵ���ϵͳ����������
D. ����ʱ�̣�������a��b������˲ʱ���ʴ�С���
���𰸡�BD
��������
ͨ����ʼʱ��a��b�����ʹ�����ֹ��a���ܴ��ʹ�Ħ�������ã����ݹ�����ƽ��ó�a��b��������ϵ������b�����ĸ߶ȵó�a�½��ĸ߶ȣ��Ӷ����a�������ܵļ�С�������������غ㶨���ж�Ħ��������a��b�����Լ���е�ܵĹ�ϵ��
A���ʼʱ��a��b�����ʹ�����ֹ��a���ܴ��ʹ�Ħ�������ã���magsin��=mbg����![]() b�½�h����a����hsin�ȣ���a�������ܵ�������Ϊmag��hsin��=mgh����A����
b�½�h����a����hsin�ȣ���a�������ܵ�������Ϊmag��hsin��=mgh����A����
B����������غ�ã�ϵͳ��е�����ӣ�Ħ������a���Ĺ�����a��b��е�ܵ���������B��ȷ��
C��������غ�ô��ʹ���������a�����ĵĵ��ܵ���ϵͳ���������ܺ�ϵͳ���ܵ����ӣ���C����
D�����ʱ��a��b��������ȣ���b��������˲ʱ����Pb=mgv����a�У�Pa=magvsin��=mgv������������a��b������˲ʱ���ʴ�С��ȣ���D��ȷ��
��ѡ��BD��