题目内容
【题目】如图所示，半径为r=0.4m的1/4圆形光滑轨道AB固定于竖直平面内，轨道与粗糙的水平地面相切于B点，CDE为固定于竖直平面内的一段内壁光滑的中空方形细管，DE段被弯成以O为圆心、半径R=0.2m的一小段圆弧，管的C端弯成与地面平滑相接，O点位于地面，OE连线竖直．可视为质点的物块b，从A点由静止开始沿轨道下滑，经地面进入细管（b横截面略小于管中空部分的横截面），b滑到E点时受到细管下壁的支持力大小等于所受重力的1/2．已知物块b的质量m = 0.4kg，g取10m/s2．
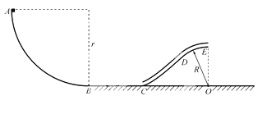
（1）求物块b滑过E点时的速度大小vE．
（2）求物块b滑过地面BC过程中克服摩擦力做的功Wf．
（3）若将物块b静止放在B点，让另一可视为质点的物块a，从A点由静止开始沿轨道下滑，滑到B点时与b发生弹性正碰，已知a的质量M≥m，求物块b滑过E点后在地面的首次落点到O点的距离范围．
【答案】(1)1m/s(2) 
(3) 0.2m≤x＜1m
【解析】
试题（1）物块b滑过E点时重力和支持力的合力提供向心力，根据牛顿第二定律得
（2分）代入 
联立解得 
（1分）
（2）物块b从A点到E点的过程中，由动能定理得
（2分）
解得 （1分）
（3）物块a从A滑到B的过程机械能守恒，设物块a滑到B点时速度为v，则有
（1分）
解得 
设碰撞后物块a、b的速度分别为va、vb，碰撞过程由动量守恒和机械能守恒得
（2分）
（2分）
联立解得 
因为M≥m，由上式可知，
碰撞后v≤vb＜2v，即
m/s≤vb＜
m/s （2分）
物块b从B点到E点的过程中，由动能定理得
（2分）
物块b离开E点后做平抛运动，设时间为t，首次落点到O点的距离为x，则有
（1分）
（1分）
由以上三式联立解得 0.2m≤x＜1m（1分）
练习册系列答案
相关题目
