题目内容
【题目】在科学研究中，可以通过施加适当的磁场来实现对带电粒子运动的控制．在如图所示的平面坐标系xOy内，矩形区域(－3d<x<d、－
d<y<d)外存在范围足够大的匀强磁场．一质量为m、电荷量为＋q的粒子从P(0，d)点沿y轴正方向射入磁场，当入射速度为v0时，粒子从(－2d，d)处进入无场区，不计粒子重力．
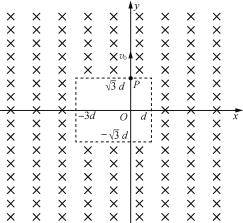
（1）求磁场的磁感应强度B的大小；
（2）求粒子离开P点后经多长时间第一次回到P点；
（3）若仅将入射速度变为2v0，求粒子离开P点后运动多少路程经过P点．
【答案】（1）
（2）
（3）
，其中k＝1、2、3…
或
，其中k＝0、1、2、3
【解析】
（1）找出半径，根据洛伦兹力提供向心力进行求解即可；
（2）画出粒子运动轨迹，求出在磁场中运动时间和在无磁场中运动的时间；
（3）画出粒子运动轨迹，注意讨论粒子运动的方向不同；
（1）由题条件可判断粒子做圆周运动半径为：
粒子在磁场中
，得到：
；
（2）粒子运动轨迹如图所示：
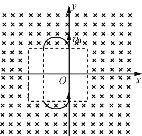
粒子在磁场中运动时间：
粒子在无场区运动时间：
粒子再次回到P点时间：
得到：
（3）粒子运动轨迹如图所示：
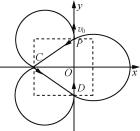
粒子速度变为
，则在磁场中运动半径为：
由P点沿圆弧运动到C点时间：
由C点沿直线运动到D点时间：
①粒子以2v0沿y轴正向经过P
则粒子运动时间：
，其中k＝1、2、3…
粒子运动距离：
得到：，其中k＝1、2、3…
②粒子以大小与－y方向成60°经过P
则：
，其中k＝0、1、2、3…
粒子运动距离为：
得到：，其中k＝0、1、2、3…
练习册系列答案
尖子生新课堂课时作业系列答案
英才计划同步课时高效训练系列答案
相关题目
