题目内容
【题目】某人在静水中划行速度
,若他在水速
的河中匀速划行.求:
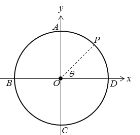
（1）.他怎样划行才能使他在最短时间内到达对岸?最短时间为多少?
（2）.若要使船的实际划行轨迹最短,他应该怎样划行?最短轨迹为多少?(d=90m)
【答案】（1）50s （2）与河岸之间的夹角是53° 150m
【解析】
（1）欲使船渡河时间最短，船头应与河岸垂直，故最短时间为: 
；
（2）由于船在静水中的速度小于水的速度，所以船的实际的轨迹不可能垂直于河岸到达；需要船头的方向偏向上游；
设船头与河岸之间的夹角为θ，则满足：v1=v2cosθ时，实际速度与河岸之间的夹角最大，到达对岸的航程最短；
代入数据得：θ=53°
最短距离：
答案：（1）他船头应与河岸垂直可以在最短时间内到达对岸，最短时间是50s．
（2）若要使船沿轨迹最短过河，应船头的方向偏向上游，与河岸之间的夹角是53°划行，对应的最短轨迹为是150m．
练习册系列答案
阅读快车系列答案
相关题目
