题目内容
如图所示，总质量为m的滑雪者以初速度V0沿倾角为θ的斜面向上自由滑行，雪橇与斜面间动摩擦因数为?，重力加速度为g，假设斜面足够长．不计空气阻力．试求：（1）滑雪者沿斜面上滑的加速度大小．
（2）滑雪者沿斜面上滑的最大距离．
（3）若滑雪者滑至最高点后掉转方向向下自由滑行，求沿斜面自由下滑的加速度大小．
分析：（1）滑雪者向上做匀减速直线运动，对其受力分析，求得加速度．
（2）由匀变速运动位移公式可以得到上滑的距离．
（3）向下自由滑行移做匀加速直线运动，然后受力分析，到加速度．
（2）由匀变速运动位移公式可以得到上滑的距离．
（3）向下自由滑行移做匀加速直线运动，然后受力分析，到加速度．
解答：解：（1）上滑过程中，对人进行受力分析，滑雪者受重力mg，弹力FN，摩擦力f，并设滑雪者的加速度为a1，受力如图
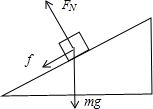
根据牛顿第二定律有：
mgsinθ+f=ma1，①
N=mgcosθ
又f=?N
求得：a1=g（sinθ+?cosθ）
（2）滑雪者沿斜面向上做匀减速直线运动，则有 v02=2a1x
得 x=
（3）滑雪者沿斜面向下做匀加速直线运动，受力如图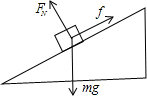
根据牛顿第二定律得 mgsinθ-?mgcosθ=ma2
求得a2=g（sinθ-?cosθ）
答：
（1）滑雪者沿斜面上滑的加速度大小是g（sinθ+?cosθ）．
（2）滑雪者沿斜面上滑的最大距离是
．
（3）若滑雪者滑至最高点后掉转方向向下自由滑行，沿斜面自由下滑的加速度大小是g（sinθ-?cosθ）．
根据牛顿第二定律有：
mgsinθ+f=ma1，①
N=mgcosθ
又f=?N
求得：a1=g（sinθ+?cosθ）
（2）滑雪者沿斜面向上做匀减速直线运动，则有 v02=2a1x
得 x=
| ||
| 2g(sinθ+μcosθ) |
（3）滑雪者沿斜面向下做匀加速直线运动，受力如图
根据牛顿第二定律得 mgsinθ-?mgcosθ=ma2
求得a2=g（sinθ-?cosθ）
答：
（1）滑雪者沿斜面上滑的加速度大小是g（sinθ+?cosθ）．
（2）滑雪者沿斜面上滑的最大距离是
| ||
| 2g(sinθ+μcosθ) |
（3）若滑雪者滑至最高点后掉转方向向下自由滑行，沿斜面自由下滑的加速度大小是g（sinθ-?cosθ）．
点评：本题是牛顿第二定律和运动学公式的综合应用问题，加速度是关键量，是必求的量，也可以根据动能定理求解上滑的最大距离．
练习册系列答案
相关题目
如图所示，总质量为m=75kg的滑雪者以初速度v0=8m/s沿倾角为θ=37°的斜面向上自由滑行，已知雪橇与斜面问动摩擦因数μ=0.25，假设斜面足够长．不计空气阻力．试求：
如图所示，总质量为M的气缸放在地面上，活塞连同手柄的质量为m，活塞的截面积为S，大气压强为p0．当气缸竖直放置时，气缸内空气压强为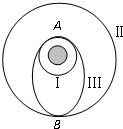
（2006?宜昌模拟）如图所示，总质量为m的飞船绕地球在半径为r1的圆轨道Ⅰ上运行，要进入半径为r2的更高的圆轨道Ⅱ，必须先加速进入一个椭圆轨道Ⅲ，然后再进入圆轨道Ⅱ．轨道Ⅰ、Ⅲ相切于A点．已知飞船在圆轨道Ⅱ上运动速度大小为v，在A点通过发动机向后以速度大小为u（对地）喷出一定质量气体，使飞船速度增加到v’进入椭圆轨道Ⅲ．（已知量为m、r1、r2、v、v′、u）求：
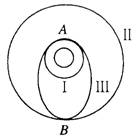如图所示，总质量为m的飞船绕地球在半径为
的圆轨道I上运行，要进入半径为
的更高的圆轨道II，必须先加速进入一个椭圆轨道III，然后再进入圆轨道II。轨道I、III相切于A点。已知飞船在圆轨道II上运动速度大小为
，在A点通过发动机向后以速度大小为
（对地）喷出一定质量气体，使飞船速度增加到
进入椭圆轨道III。（已知量为
）求：
；（2）发动机喷出气体的质量。