题目内容
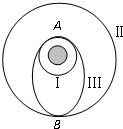 (2006?宜昌模拟)如图所示,总质量为m的飞船绕地球在半径为r1的圆轨道Ⅰ上运行,要进入半径为r2的更高的圆轨道Ⅱ,必须先加速进入一个椭圆轨道Ⅲ,然后再进入圆轨道Ⅱ.轨道Ⅰ、Ⅲ相切于A点.已知飞船在圆轨道Ⅱ上运动速度大小为v,在A点通过发动机向后以速度大小为u(对地)喷出一定质量气体,使飞船速度增加到v’进入椭圆轨道Ⅲ.(已知量为m、r1、r2、v、v′、u)求:
(2006?宜昌模拟)如图所示,总质量为m的飞船绕地球在半径为r1的圆轨道Ⅰ上运行,要进入半径为r2的更高的圆轨道Ⅱ,必须先加速进入一个椭圆轨道Ⅲ,然后再进入圆轨道Ⅱ.轨道Ⅰ、Ⅲ相切于A点.已知飞船在圆轨道Ⅱ上运动速度大小为v,在A点通过发动机向后以速度大小为u(对地)喷出一定质量气体,使飞船速度增加到v’进入椭圆轨道Ⅲ.(已知量为m、r1、r2、v、v′、u)求:(1)飞船在轨道Ⅰ上的速率v1;
(2)发动机喷出气体的质量.
分析:(1)根据万有引力提供向心力,分别得出两圆轨道上线速度的大小关系,从而求出飞船在轨道Ⅰ上的速率.
(2)根据动量守恒定律求出发电机喷出气体的质量.
(2)根据动量守恒定律求出发电机喷出气体的质量.
解答:解(1)飞船在轨道Ⅰ上做匀速圆周运动,由牛顿第二定律有G
=m
,①
飞船在轨道Ⅱ上做匀速圆周运动,由牛顿第二定律G
=m
,②
由①②得v=v1
. ③
(2)由题意知,飞船在喷气过程中,运动方向上动量守恒,mv1=(m-△m)v'-△mu,④
由③④得△m=
m.
答:(1)飞船在轨道Ⅰ上的速率v=v1
.
(2)发动机喷出气体的质量△m=
m.
| Mm | ||
|
| ||
| r1 |
飞船在轨道Ⅱ上做匀速圆周运动,由牛顿第二定律G
| Mm | ||
|
| ||
| r2 |
由①②得v=v1
|
(2)由题意知,飞船在喷气过程中,运动方向上动量守恒,mv1=(m-△m)v'-△mu,④
由③④得△m=
v′-v
| ||||
| v′+u |
答:(1)飞船在轨道Ⅰ上的速率v=v1
|
(2)发动机喷出气体的质量△m=
v′-v
| ||||
| v′+u |
点评:本题考查了万有引力提供向心力这一理论,以及动量守恒定律,难度中等,平时的练习中需加强训练.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2006?宜昌模拟)如图所示,半圆形玻璃砖的半径为R,直径MN,一细束白光从Q点垂直于直径MN的方向射入半圆形玻璃砖,从玻璃砖的圆弧面射出后,打到光屏P上,得到由红到紫的彩色光带.已知QM=
(2006?宜昌模拟)如图所示,半圆形玻璃砖的半径为R,直径MN,一细束白光从Q点垂直于直径MN的方向射入半圆形玻璃砖,从玻璃砖的圆弧面射出后,打到光屏P上,得到由红到紫的彩色光带.已知QM=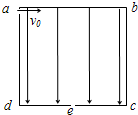 (2006?宜昌模拟)如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场.一个质量为m带正电粒子(重力不计)从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出.求:
(2006?宜昌模拟)如图所示,abcd是一个正方形盒子.cd边的中点有一个小孔e.盒子中有沿ad方向的匀强电场.一个质量为m带正电粒子(重力不计)从a处的小孔沿ab方向以初速度v0射入盒内,并恰好从e处的小孔射出.求: (2006?宜昌模拟)如图所示,光滑绝缘水平面的上方空间被竖直的分界面MN分隔成两部分,左侧空间存在一水平向右的匀强电场,场强大小 E1=
(2006?宜昌模拟)如图所示,光滑绝缘水平面的上方空间被竖直的分界面MN分隔成两部分,左侧空间存在一水平向右的匀强电场,场强大小 E1=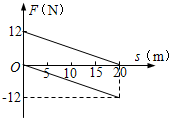 (2006?宜昌模拟)一物体静止在光滑水平面上,同时受到两个水平拉力F1、F2的作用,Fl、F2与位移的关系如图所示,则物体出现动能最大值时物体发生的位移大小应为( )
(2006?宜昌模拟)一物体静止在光滑水平面上,同时受到两个水平拉力F1、F2的作用,Fl、F2与位移的关系如图所示,则物体出现动能最大值时物体发生的位移大小应为( )