题目内容
（2000?上海）一小球用轻绳悬挂在某固定点，现将轻绳水平拉直，然后由静止开始释放小球．考虑小球由静止开始运动到最低位置的过程（ ）
分析：对小球进行受力分析，分析水平方向受力情况就可得到水平速度的变化，竖直方向速度抓住初末位置竖直方向速度都为0，即可判断，根据动能定理判断最低点线速度是否最大，到达最低点时，具有向上的向心加速度，故拉力大于重力．
解答：解：对小球进行受力分析，如图所示：
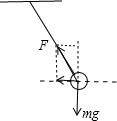
A、小球受到绳子拉力的水平分量始终对小球做正功，所以小球水平方向速度逐渐增大，故A正确；
B、小球由静止开始运动时竖直方向速度为0，到最低位置时竖直方向速度还是0，所以小球在竖直方向的速度先增大后减小，故B错误；
C、整个下摆过程中，只有重力做功，故势能不断转化为动能，所以小球在最低点动能最大，故C正确；
D、小球经最低点时，具有向上的向心加速度，故拉力大于重力，故D错误．
故选AD．
A、小球受到绳子拉力的水平分量始终对小球做正功，所以小球水平方向速度逐渐增大，故A正确；
B、小球由静止开始运动时竖直方向速度为0，到最低位置时竖直方向速度还是0，所以小球在竖直方向的速度先增大后减小，故B错误；
C、整个下摆过程中，只有重力做功，故势能不断转化为动能，所以小球在最低点动能最大，故C正确；
D、小球经最低点时，具有向上的向心加速度，故拉力大于重力，故D错误．
故选AD．
点评：本题考查了功与能量转换的关系以及竖直平面内的圆周运动在最低点合外力提供向心力等知识点，难度适中．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
（2000?上海）如图为一名宇航员“漂浮”在地球外层空间的照片，根据照片展现的情景提出两个与物理知识有关的问题（所提的问题可以涉及力学、电磁学、热学、光学、原子物理学等各个部分，只需提出问题，不必作出回答和解释）：