��Ŀ����
����Ŀ����ͼ��ʾ�����㹻��ƽ�й⻬�Ľ�������MN��PQ���ΪL������ƽ����ˮƽ��нǦ�=30�㣬������費�ƣ��Ÿ�Ӧǿ��ΪB����ǿ�ų���ֱ����ƽ�����ϣ���ΪL�Ľ�����ab��ֱ��MN��PQ�����ڵ����ϣ���ʼ���뵼��Ӵ����ã�������������Ϊm������ΪR��������������϶������Ҷ˵�·�����ݵĵ���RL=4R����ֵ����R1=2R��������������ʹR2=12R���������ٶ�Ϊg���ֽ��������ɾ�ֹ�ͷţ�����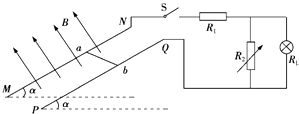
��1���������»�������ٶ�Ϊ���
��2�����������»�����ΪS0ʱ�ٶ�ǡ�ôﵽ�����������ɾ�ֹ��ʼ�»�2S0�Ĺ����У�������·�����Ľ�����Q��
���𰸡�
��1���⣺�������������»�ʱ�ٶ����������ٶ�Ϊvm���ﵽ���ʱ�������ƽ��������
mgsin��=F��
�� F��=ILB��I= ![]() ��E=BLvm
��E=BLvm
R��=R1+ ![]() +R=2R+
+R=2R+ ![]() +R=6R
+R=6R
�����������ٶȣ�vm= ![]()
��2���⣺�������غ�֪��mg2S0sin30��=Q+ ![]()
��ã�Q=mgS0�� ![]() =mgS0��
=mgS0�� ![]()
����������1��������ab�ȼ����»������ܵİ����������ٶȼ�С���������»����ٶȴﵽ����ɱպϵ�·ŷķ���ɡ���Ӧ�綯�ƺͰ�������ʽ�Ƶ����������ı���ʽ������ƽ�������������ٶȣ���2�����������»�ֱ���ٶȴﵽ���Ĺ����У��������Ļ�е�ܼ�Сת��Ϊ���ܣ����������غ㶨��������Q��
�����㾫����������Ĺؼ���������ܶ������ۺ�Ӧ�õ����֪ʶ������Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ��Լ��������غ㶨�ɵ����⣬�˽������غ㶨�ɣ������Ȳ�������Ҳ���ᴴ������ֻ���һ����ʽת��Ϊ������ʽ�����ߴ�һ������ת�Ƶ���һ�����壬����ת����ת�ƹ����У��������������ֲ��䣮