题目内容
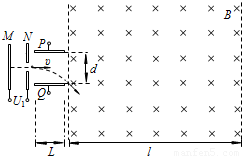
 如图所示,M、N为正对着竖直放置的金属板,其中N板的正中央有一个小孔,M、N板间的电压 U1=1.0×103V.P、Q为正对着水平放置的金属板,板长L=10cm,两板间的距离 d=12cm,两板间的电压 U2=2.4×103V.P、Q板的右侧存在方向垂直纸面向里的匀强磁场区域,其中虚线为磁场的左右边界,边界之间的距离l=60cm,竖直方向磁场足够宽.一个比荷
如图所示,M、N为正对着竖直放置的金属板,其中N板的正中央有一个小孔,M、N板间的电压 U1=1.0×103V.P、Q为正对着水平放置的金属板,板长L=10cm,两板间的距离 d=12cm,两板间的电压 U2=2.4×103V.P、Q板的右侧存在方向垂直纸面向里的匀强磁场区域,其中虚线为磁场的左右边界,边界之间的距离l=60cm,竖直方向磁场足够宽.一个比荷| q | m |
(1)求粒子进入P、Q板间时速度 υ 的大小;
(2)若粒子进入磁场后,恰好没有从磁场的右边界射出,求匀强磁场的磁感应强度B的大小.
分析:粒子在MN间加速,由动能定理有:qU=
mv2,在MN间加速后,以速度v进入PQ,并在PQ间偏转,粒子做类平抛运动,射出PQ时速度v′,最后在磁场中以速度v′做匀速圆周运动.运动轨迹恰与磁场右边界相切.
| 1 |
| 2 |
解答: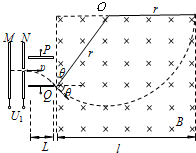 解:(1)粒子在M、N间运动时,根据动能定理得qU1=
解:(1)粒子在M、N间运动时,根据动能定理得qU1=
mυ2
带入数据得:v=
=104m/s
粒子进入P、Q板间时速度为104m/s;
(2)设粒子在P、Q板间运动的时间为t.
粒子的加速度 a=
粒子在竖直方向的速度 υy=at
粒子的水平位移 L=υt
若粒子穿出P、Q板间时速度偏向角为θ,则tanθ=
=
=1
所以θ=45°.
粒子穿出P、Q板间时的速度υ1=
υ
粒子在匀强磁场中做匀速圆周运动时,轨迹如上图所示,粒子进入磁场时速度的大小为υ1,速度的方向与水平方向的夹角也为θ,所以rsinθ+r=l
因为洛伦兹力提供向心力,则qυ1B=m
解得 B=0.8 T
匀强磁场的磁场强度为0.8T
 解:(1)粒子在M、N间运动时,根据动能定理得qU1=
解:(1)粒子在M、N间运动时,根据动能定理得qU1=| 1 |
| 2 |
带入数据得:v=
|
粒子进入P、Q板间时速度为104m/s;
(2)设粒子在P、Q板间运动的时间为t.
粒子的加速度 a=
| qU2 |
| md |
粒子在竖直方向的速度 υy=at
粒子的水平位移 L=υt
若粒子穿出P、Q板间时速度偏向角为θ,则tanθ=
| υy |
| υ |
| U2L |
| 2dU1 |
所以θ=45°.
粒子穿出P、Q板间时的速度υ1=
| 2 |
粒子在匀强磁场中做匀速圆周运动时,轨迹如上图所示,粒子进入磁场时速度的大小为υ1,速度的方向与水平方向的夹角也为θ,所以rsinθ+r=l
因为洛伦兹力提供向心力,则qυ1B=m
| υ12 |
| r |
解得 B=0.8 T
匀强磁场的磁场强度为0.8T
点评:在此题中注意分清过程,弄清每个过程中的物理模型.运用相应知识点来逐一解决.更要注意题目中的恰好的含义.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目

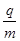 = 5.0×104 C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.
= 5.0×104 C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.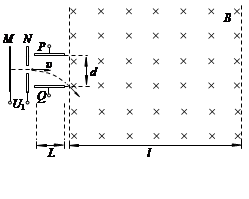
 = 5.0×104 C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.
= 5.0×104 C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.
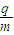 =5.0×104C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.
=5.0×104C/kg的带正电粒子,从静止开始经M、N板间的电压U1加速后,沿P、Q板间的中心线进入P、Q间,并最终进入磁场区域.整个装置处于真空中,不计重力影响.