题目内容
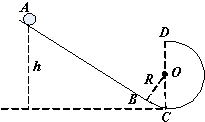
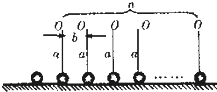
如图所示，长为a的轻质细线，一端悬挂在O点，另一端接一质量为m的小球，组成一个能绕O点自由转动的振子，现有n个这样的振子以相等的间隔b（b＞2a）成一直线悬于光滑的平台上，且悬点距台面的高度均为a，今有一质量为m的小球以水平速度v沿台面射向振子，且与振子碰撞时无能量损失，为使每个振子被小球碰后都能在竖直面内转一周，则入射小球的速度不能小于（ ）
A．
| B．2
| C．
| D．
|
由于小球与振子碰撞无能量损失，每次小球与振子、振子与小球碰撞后均交换速度．振子完成完整圆周运动在最低点的最小速度应为v0，则根据机械能守恒得：
m
=mg?2a+
mv2，
振子刚好到达最高点时，有：mg=m
，
所以可解得：v0=
，
因此，只有入射小球的速度不小于 v0=
，就可使所有振子完成完整的圆周运动．故C正确．
故选：C
| 1 |
| 2 |
| v | 20 |
| 1 |
| 2 |
振子刚好到达最高点时，有：mg=m
| v2 |
| a |
所以可解得：v0=
| 5ag |
因此，只有入射小球的速度不小于 v0=
| 5ag |
故选：C
练习册系列答案
名校课堂系列答案
相关题目
