Question

【题目】在如图所示，AB为光滑水平桌面；BQ为竖直平面内半径为R的四分之一粗糙圆弧轨道，固定在AB右端。Q点与圆心O等高。在水平桌面上放一块长为L=1m的木板，其质量为m=1kg，木板右端上表面与圆弧轨道相切于B点。木板左端放一个质量也为m的小物块（可视为质点），小物块带电量为。现在竖直线OB左侧空间加匀强电场，电场强度E=105 N/C，方向与水平方向成370斜向下，同时在小物块上施加6N的水平向左的恒力F。小物块与木板之间的动摩擦因数为μ=0.25，重力加速度g=10m/s2。sin370 = 0.6，cos370 = 0.8。设小物块与薄板间的最大静摩擦力等于滑动摩擦力。

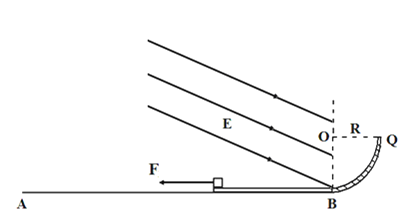
（1）求小物块所受的摩擦力大小；

（2）若撤去拉力F，求小物块第一次到达B点时的速度大小；

（3）当小物块返回B点时，撤去电场。小物块最后停在木板上，距木板右端l=0.2m处。 求小物块在圆弧轨道上运动过程中克服摩擦力做的功。

Answer 1

【答案】（1） （2） （3）

【解析】（1）电场力在水平方向的分力为：qEcos37°=10-4×105×0.8=8N
电场力在竖直方向的分力为：qEsin37°=10-4×105×0.6=6N
小物块与木板间的最大静摩擦力为：fm=μ（mg+qEsin37°）=0.25×（1×10+6）=4N
由于qEcos37°-F＜fm，小物块保持静止，
所以小物块受静摩擦力为：f=qEcos37°-F=8-6=2N
（2）撤去F后，小物块向右加速，木板仍然静止．小物块受合力为：
F=qEcos37°-fm=8-4=4N，
小物块从开始至运动到B点，由动能定理得：Fl=mv02
B点速度为：

代入数据解得：v0=2m/s
（3）小物块从B点滑上圆弧轨道后再返回B点过程，设返回速度为v，由动能定理有：
-Wf=mv2mv02
小物块减速，加速度大小为：a1= =μg=2.5m/s2；
木板加速，加速度大小为：a2==μg=2.5m/s2
从小物块滑上木板到相对静止，所用时间为t，有：v-a1t=a2t
（vt-a1t2）-a2t2=l
解得：Wf=3J