题目内容
2. 如图所示,B为竖直圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α,一小球在圆轨道左侧的A点以速度v0平抛,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,则由此可求出( )
如图所示,B为竖直圆轨道的左端点,它和圆心O的连线与竖直方向的夹角为α,一小球在圆轨道左侧的A点以速度v0平抛,恰好沿B点的切线方向进入圆轨道,已知重力加速度为g,则由此可求出( )| A. | AB间的水平距离 | B. | AB间的竖直距离 | ||
| C. | 小球从A到B的飞行时间 | D. | 小球在C点对轨道的压力 |
分析 根据小球恰好从轨道的B端沿切线方向进入轨道,说明小球通过B点的速度沿着B点切线方向,从而可以根据速度分解求得经过B点时竖直方向分速度,进而求出运动的时间,根据水平方向上的运动规律求出AB间的水平距离.由机械能守恒求出小球经过C点时的速度,由牛顿运动定律求小球对轨道的压力.
解答 解:ABC、小球经过B点时的速度沿B点的切线方向,与水平方向的夹角为α.
根据平行四边形定则知,小球通过B点时竖直方向上的分速度 vy=v0tanα.
则小球从A到B的飞行时间 t=$\frac{{v}_{y}}{g}$=$\frac{{v}_{0}tanα}{g}$.
则AB间的水平距离 x=v0t=$\frac{{v}_{0}^{2}tanα}{g}$
AB间的竖直距离 y=$\frac{{v}_{y}^{2}}{2g}$=$\frac{{v}_{0}^{2}ta{n}^{2}α}{2g}$
从A到C,由机械能守恒得:mg[y+R(1-cosα)]=$\frac{1}{2}m{v}_{B}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
在C点,由牛顿第二定律得:N-mg=m$\frac{{v}_{B}^{2}}{R}$
由于轨道半径R未知,所以不能求N,也不能得到小球在C点对轨道的压力.故ABC正确,D错误.
故选:ABC.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,运用运动的分解研究平抛运动.

练习册系列答案
相关题目
13.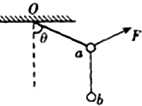 如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
 如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )
如图所示,将两个质量均为m的小球a、b用细线相连并悬挂于O点,用力F拉小球a使整个装置处于平衡状态,且悬线Oa与竖直方向的夹角为θ=60°,则力F的大小可能为 ( )| A. | $\sqrt{3}$mg | B. | mg | C. | $\frac{\sqrt{3}}{2}$mg | D. | $\frac{\sqrt{3}}{3}$Lmg |
10.如图所示为A、B、C三个小球做平抛运动的示意图,关于三个球做平抛运动的判断正确的是( )


| A. | 三个球抛出初速度大小关系为vA>vB>vC | |
| B. | 若三个球同时抛出,则C球先落地 | |
| C. | 若三个球同时落地,则A球先抛出 | |
| D. | 若某一时刻三个球在同一竖直线上,则A球一定在最下面 |
17.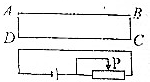 如图所示,要使线圈ABCD中产生顺时针方向的感应电流,可采用的方法是( )
如图所示,要使线圈ABCD中产生顺时针方向的感应电流,可采用的方法是( )
 如图所示,要使线圈ABCD中产生顺时针方向的感应电流,可采用的方法是( )
如图所示,要使线圈ABCD中产生顺时针方向的感应电流,可采用的方法是( )| A. | 变阻器触点P向左移动或线圈ABCD向上平移 | |
| B. | 变阻器触点P向右移动或线圈ABCD向下平移 | |
| C. | 变阻器触点P向左移动或线圈ABCD向下平移 | |
| D. | 变阻器触点P向右移动或线圈ABCD向上平移 |

 匀强电场和匀强磁场均关于y轴对称分布,在如图所示的直角坐标系中,相邻的电场和磁场宽度均为L,各电场区域内电场强度大小相等,各磁场区域内磁感应强度大小也相等,电场和磁场方向如图所示.在A(-1.5L,0.5L)处电荷量为+q、质量为m的粒子,从t=O时刻起以速度v0沿x轴正方向射出,粒子刚好从C(-0.5L,0)点进入磁场,并从D(0.5L,0)点射出磁场进入电场,不计粒子的重力及电场或磁场的边缘效应,求:
匀强电场和匀强磁场均关于y轴对称分布,在如图所示的直角坐标系中,相邻的电场和磁场宽度均为L,各电场区域内电场强度大小相等,各磁场区域内磁感应强度大小也相等,电场和磁场方向如图所示.在A(-1.5L,0.5L)处电荷量为+q、质量为m的粒子,从t=O时刻起以速度v0沿x轴正方向射出,粒子刚好从C(-0.5L,0)点进入磁场,并从D(0.5L,0)点射出磁场进入电场,不计粒子的重力及电场或磁场的边缘效应,求: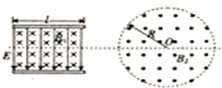 如图所示,一速度选择中电场的方向和磁场的方向分别是竖直向下和垂直于纸面向里,电场强度和磁感应强度的大小分别为E=2×104N/C和B1=0.1T,极板的长度l=$\frac{\sqrt{3}}{3}$m,间距足够大,在板的右侧还存在着另一圆形区域的匀强磁场,磁场的方向为垂直于纸面向外,圆形区域的圆心O位于平行金属极板的中线上,圆形区域的半径R=$\frac{\sqrt{3}}{3}$m,有一带正电的粒子以某速度沿极板的中线水平向右射入极板后恰好做匀速直线运动,然后进入圆形磁场区域,飞出圆形磁场区域时速度方向偏转了60°,不计粒子的重力,粒子的比荷$\frac{q}{m}$=2×103C/kg.
如图所示,一速度选择中电场的方向和磁场的方向分别是竖直向下和垂直于纸面向里,电场强度和磁感应强度的大小分别为E=2×104N/C和B1=0.1T,极板的长度l=$\frac{\sqrt{3}}{3}$m,间距足够大,在板的右侧还存在着另一圆形区域的匀强磁场,磁场的方向为垂直于纸面向外,圆形区域的圆心O位于平行金属极板的中线上,圆形区域的半径R=$\frac{\sqrt{3}}{3}$m,有一带正电的粒子以某速度沿极板的中线水平向右射入极板后恰好做匀速直线运动,然后进入圆形磁场区域,飞出圆形磁场区域时速度方向偏转了60°,不计粒子的重力,粒子的比荷$\frac{q}{m}$=2×103C/kg.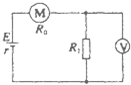 如图所示的电路中,电源电动势E=20V,内阻r=0.5Ω,电动机的电阻R0=0.5Ω,电阻R1=1Ω,电动机正常工作时,电压表的示数U1=4V,求:
如图所示的电路中,电源电动势E=20V,内阻r=0.5Ω,电动机的电阻R0=0.5Ω,电阻R1=1Ω,电动机正常工作时,电压表的示数U1=4V,求: