题目内容
7.小船渡过一条河流,当船头垂直对岸方向出发时,在出发后的600s到达对岸下游120m处,若船头保持与河岸成α角向上游出发,在出发后750s时到达正对岸.求:(1)水流的速度;
(2)船在静水中的速度;
(3)河的宽度;
(4)船头与河岸的夹角α.
分析 将船的运动分解为垂直于河岸和沿河岸方向,抓住分运动与合运动具有等时性求出河的宽度.
解答 解:(1)设静水速为v1,水流速为v2.船头保持跟河岸垂直的方向航行时有:v1t=120m,
则有:v2=$\frac{120}{600}$s=0.2m/s
(2、3)而v1t=d,当合速度与河岸垂直时,合速度为:
v=$\sqrt{{v}_{1}^{2}-{v}_{2}^{2}}$,
且d=vt′.
联立以上各式解得:d=200m,v1=$\frac{1}{3}m/s$.
(4)斜着航线时,船的速度为:v1sinα=$\frac{d}{12.5×60}$;
因$sinα=\frac{200}{12.5×60×\frac{1}{3}}=0.8$
解得:α=53°;
答:(1)水流的速度0.2m/s,
(2)船在静水中的速度$\frac{1}{3}$m/s,
(3)河的宽度200m,
(4)船头与河岸间的夹角α=53°.
点评 解决本题的关键知道分运动与合运动具有等时性,各分运动具有独立性,互不干扰,注意列出方程组,从而求解是解题的基本思路.

练习册系列答案
相关题目
18.一个物体做匀减速直线运动,初速度为20m/s,加速度大小为4m/s2,则物体在停止运动前3s内的平均速度为( )
| A. | 4 m/s | B. | 6 m/s | C. | 8m/s | D. | 10 m/s |
2.电动自行车因其价格相对于摩托车低廉,而且污染小,受到群众喜爱,某电动车铭牌如下表所 示.取g=10m/s2,试求
(1)求此车所装电动机的线圈电阻.
(2)求此车所装电动机在额定电压下正常工作时的效率.
(3)一个60kg的人骑着此车,如果电动自行车所受阻力为人和车重的0.02倍,求电动自行车在平直公路上行驶的最大速度.
| 规格 | 后轮驱动直流永磁电机 |
| 车型:20′′电动自行车 | 电机输出功率:175W |
| 电源输出电压:≥36V | 额定工作电压/电流:36V/5A |
| 整车质量:40kg | 最大载重量:120kg |
(2)求此车所装电动机在额定电压下正常工作时的效率.
(3)一个60kg的人骑着此车,如果电动自行车所受阻力为人和车重的0.02倍,求电动自行车在平直公路上行驶的最大速度.
9. 如图所示,在方向垂直向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框dc边始终与磁场右边界平行,线框边长ad=L,cd=2L,线框导线的总电阻为R,则线框离开磁场的过程中( )
如图所示,在方向垂直向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框dc边始终与磁场右边界平行,线框边长ad=L,cd=2L,线框导线的总电阻为R,则线框离开磁场的过程中( )
 如图所示,在方向垂直向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框dc边始终与磁场右边界平行,线框边长ad=L,cd=2L,线框导线的总电阻为R,则线框离开磁场的过程中( )
如图所示,在方向垂直向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框以恒定的速度v沿垂直磁场方向向右运动,运动中线框dc边始终与磁场右边界平行,线框边长ad=L,cd=2L,线框导线的总电阻为R,则线框离开磁场的过程中( )| A. | ad间的电压为$\frac{BLv}{3}$ | |
| B. | 线框所受安培力的合力为$\frac{2{B}^{2}{L}^{2}v}{R}$ | |
| C. | 流过线框截面的电量为$\frac{2B{L}^{2}}{R}$ | |
| D. | 线框中的电流在ad边产生的热量为$\frac{2{B}^{2}{L}^{3}v}{3R}$ |
 在“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图.
在“验证力的平行四边形定则”的实验情况如图甲所示,其中A为固定橡皮筋的图钉,O为橡皮筋与细绳的结点,OB和OC为细绳.图乙是在白纸上根据实验结果画出的图. 在如图中滑动变阻器作分压器使用,负载电阻R一端接在变阻器的固定端AC上,另一端接在滑动变阻器P上,滑动端P在AB间移动时,R上就得到不同的电压.
在如图中滑动变阻器作分压器使用,负载电阻R一端接在变阻器的固定端AC上,另一端接在滑动变阻器P上,滑动端P在AB间移动时,R上就得到不同的电压. 为了测量一伏特表V的电阻Rx,某同学设计了如图所示的电路,图中电流表为微安电流表,R0和Rx分别为滑动变阻器和电阻箱,S1和S2分别是单刀开关和单刀双掷开关,E是电池.
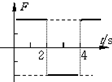
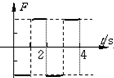
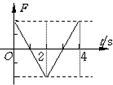
为了测量一伏特表V的电阻Rx,某同学设计了如图所示的电路,图中电流表为微安电流表,R0和Rx分别为滑动变阻器和电阻箱,S1和S2分别是单刀开关和单刀双掷开关,E是电池.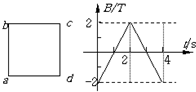 矩形导线框abcd放在匀强磁场中,磁感线方向与线圈平面垂直,磁感应强度B随时间变化的图象如图所示.t=0时刻,磁感应强度的方向垂直于纸面向里.在0∽4s时间内,线框的ab边受力随时间变化的图象(ab边所受安培力的方向规定以向左为正方向),可能下图中的( )
矩形导线框abcd放在匀强磁场中,磁感线方向与线圈平面垂直,磁感应强度B随时间变化的图象如图所示.t=0时刻,磁感应强度的方向垂直于纸面向里.在0∽4s时间内,线框的ab边受力随时间变化的图象(ab边所受安培力的方向规定以向左为正方向),可能下图中的( )