题目内容
如图所示,在磁感应强度大小为B、方向垂直向上的匀强磁场中,有一上、下两层均与水平面平行的“U”型光滑金属导轨,在导轨面上各放一根完全相同的质量为 的匀质金属杆
的匀质金属杆 和
和 ,开始时两根金属杆位于同一竖起面内且杆与轨道垂直。设两导轨面相距为H,导轨宽为L,导轨足够长且电阻不计,金属杆单位长度的电阻为r。现有一质量为
,开始时两根金属杆位于同一竖起面内且杆与轨道垂直。设两导轨面相距为H,导轨宽为L,导轨足够长且电阻不计,金属杆单位长度的电阻为r。现有一质量为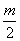 的不带电小球以水平向右的速度
的不带电小球以水平向右的速度 撞击杆
撞击杆 的中点,撞击后小球反弹落到下层面上的C点。C点与杆
的中点,撞击后小球反弹落到下层面上的C点。C点与杆 初始位置相距为S。求:
初始位置相距为S。求:
(1)回路内感应电流的最大值;
(2)整个运动过程中感应电流最多产生了多少热量;
(3)当杆 与杆
与杆 的速度比为
的速度比为 时,
时, 受到的安培力大小。
受到的安培力大小。

 的匀质金属杆
的匀质金属杆 和
和 ,开始时两根金属杆位于同一竖起面内且杆与轨道垂直。设两导轨面相距为H,导轨宽为L,导轨足够长且电阻不计,金属杆单位长度的电阻为r。现有一质量为
,开始时两根金属杆位于同一竖起面内且杆与轨道垂直。设两导轨面相距为H,导轨宽为L,导轨足够长且电阻不计,金属杆单位长度的电阻为r。现有一质量为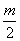 的不带电小球以水平向右的速度
的不带电小球以水平向右的速度 撞击杆
撞击杆 的中点,撞击后小球反弹落到下层面上的C点。C点与杆
的中点,撞击后小球反弹落到下层面上的C点。C点与杆 初始位置相距为S。求:
初始位置相距为S。求:(1)回路内感应电流的最大值;
(2)整个运动过程中感应电流最多产生了多少热量;
(3)当杆
 与杆
与杆 的速度比为
的速度比为 时,
时, 受到的安培力大小。
受到的安培力大小。
1)
(2)
(3)

(2)

(3)

1)对小球和杆A1组成的系统,由动量守恒定律,得:
 ①
①
又 s=vt
H= ②
②
由①②③式联立:
 ④
④
回路内感应电动势的最大值 E=BLv1 ⑤
回路内感应电流的最大值 I= ⑥
⑥
联立④⑤⑥式得:
回路内感应电流的最大值:I=
(2)对两棒组成的系统,由动量守恒定律,得:
由能量守恒定律可得整个运动过程中感应电流最多产生热量:
Q= =
=
(3)由能量守恒定律,得:
又 ∶
∶ =1∶3
=1∶3



A2受到的安培力大小

 ①
①又 s=vt
H=
 ②
②由①②③式联立:
 ④
④ 回路内感应电动势的最大值 E=BLv1 ⑤
回路内感应电流的最大值 I=
 ⑥
⑥联立④⑤⑥式得:
回路内感应电流的最大值:I=

(2)对两棒组成的系统,由动量守恒定律,得:

由能量守恒定律可得整个运动过程中感应电流最多产生热量:
Q=
 =
=
(3)由能量守恒定律,得:

又
 ∶
∶ =1∶3
=1∶3


A2受到的安培力大小



练习册系列答案
相关题目




 可沿导轨自由滑动.导轨一端连接一个定值电阻R,导轨电阻可忽略不计.现将金属棒沿导轨由静止向右拉.若保持拉力恒定,当速度为
可沿导轨自由滑动.导轨一端连接一个定值电阻R,导轨电阻可忽略不计.现将金属棒沿导轨由静止向右拉.若保持拉力恒定,当速度为 时,加速度为
时,加速度为 ,最终以速度
,最终以速度 做匀速运动;若保持拉力的功率恒定,当速度为
做匀速运动;若保持拉力的功率恒定,当速度为 ,最终也以速度
,最终也以速度






 的示数小于电流表
的示数小于电流表 的示数
的示数 、质量m=0.1kg的金属棒CD垂直跨搁在位于水平面上的两条平行光滑金属导轨上,两导轨间距也是L,棒与导轨间接触良好,导轨电阻不计.导轨左端接有
、质量m=0.1kg的金属棒CD垂直跨搁在位于水平面上的两条平行光滑金属导轨上,两导轨间距也是L,棒与导轨间接触良好,导轨电阻不计.导轨左端接有 的电阻,量程为0~3.0A的电流表串接在一条导轨上,量程为0~1.0V的电压表接在电阻R的两端,垂直导轨平面的匀强磁场垂直向下穿过平面.现以向右恒定外力F使金属棒右移.当金属棒以
的电阻,量程为0~3.0A的电流表串接在一条导轨上,量程为0~1.0V的电压表接在电阻R的两端,垂直导轨平面的匀强磁场垂直向下穿过平面.现以向右恒定外力F使金属棒右移.当金属棒以 的速度在导轨平面上匀速滑动时,观察到电路中的一个电表正好满偏,而另一个电表未满偏.问:
的速度在导轨平面上匀速滑动时,观察到电路中的一个电表正好满偏,而另一个电表未满偏.问: