题目内容
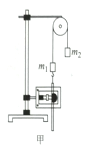
【题目】一半径为R的半圆形竖直圆柱面,用轻质不可伸长的细绳连接的A、B两球,悬挂在圆柱面边缘两侧,A球质量为B球质量的2倍,现将A球从圆柱边缘处由静止释放,如图所示,已知A球始终不离开圆柱内表面,且细绳足够长,若不计一切摩擦.求: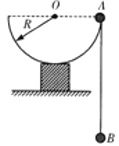
(1)A球沿圆柱内表面滑至最低点时速度的大小.
(2)从A被释放到B上升到最大高度过程中,绳子拉力对A球所做的功
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)先根据几个关系求出A球和B球速度的关系和位移的大小,再对AB整体运用机械能守恒定律即可求解;
(2)当A球的速度为0时,B上升的高度最高,则此时A球沿圆柱面运动的位移最大,设为s,则据机械能守恒定律即可求解;
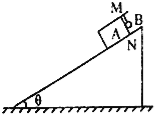
(1)当A球运动到最低点时,作出图象如图所示: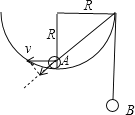
设A球的速度为v,根据几何关系可知B球的速度为![]() ,B球上升的高度为
,B球上升的高度为![]() ,
,
对AB小球整体运用系统机械能守恒得:![]()
解得:![]() ;
;
(2)当A球的速度为0时,B上升的高度最高,则此时A球沿圆柱面运动的位移最大,设为s,此时连接A球的绳子与水平方向的夹角为![]() 。
。
由几何关系得:![]()
A球下降的高度为:![]()
则据机械能守恒定律可得:![]()
解得:![]()
对A分析可知,拉力对A做功等于A的机械能的减小,即![]() 。
。

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目