��Ŀ����
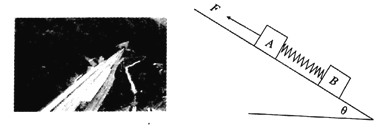
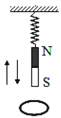
����Ŀ����ͼ��ʾ������N=20��������S=0.04 m2����Ȧ���з�����ֱ���ϵ���ǿ�ų�B1��B1���ȱ仯�����ƽ�С����ΪL=0.2m�Ľ�������̶������Ϊ30����б���ϣ�����ͨ������S����Ȧ������һ�⻬�����˷����ڿ��������϶˵�M��Nλ�ã�M��N�ȸߣ�����������m=0.02 kg����ֵR1=0.2 �������������һ��ֵΪR2=0.8 ���ĵ��裻�������������д�ֱ��б�����ϵ���ǿ�ų�B2=0.5 T���պ�S��������ǡ�ܾ�ֹ��б���M��Nλ�ã��Ͽ�S����������M��Nλ�ôӾ�ֹ��ʼ�����˶�������t=0.5 s���»�ͨ���ľ���x=0.6 m����������⻬���㹻������Ȧ�뵼��ĵ�����Բ��ơ�gȡ10 m/s2��

��1����B1�仯�ʵĴ�С����ȷ��B1�ı仯���ƣ�
��2���������»�x=0.6 m�Ĺ����У��������ϲ����Ľ����ȡ�
���𰸡���1��0.25T/s ��B1�ı仯���������� ��2��2.32��10-3J
��������
��1���պ�S������Ȧ�еĸ�Ӧ�綯��ΪE1������ΪI1���������ܵ��İ�����ΪF����
![]()
��Ӧ������![]()
��������![]() ��
��
����ƽ�������У�![]()
��ã�![]() ��B1�ı仯����������
��B1�ı仯����������
��2���Ͽ�S���������»�x=0.6 m�Ĺ����У������е�ƽ���綯��Ϊ![]() ��ƽ������Ϊ
��ƽ������Ϊ![]() ��ĩ�ٶ�Ϊv������R2�ͽ������ϲ����Ľ�����ΪQ���������ϲ����Ľ�����ΪQ1������ݶ��������У�
��ĩ�ٶ�Ϊv������R2�ͽ������ϲ����Ľ�����ΪQ���������ϲ����Ľ�����ΪQ1������ݶ��������У�
![]()
ƽ����Ӧ������
![]()
ƽ����Ӧ�綯�ƣ�
![]()
���v= 2.2 m/s
���������غ㣺
![]()
��ã�![]() J
J
![]()
��ã�![]() J��
J��