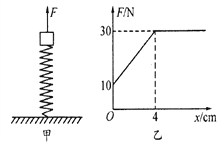
题目内容
【题目】如图a所示,一个滑雪运动员,滑板和人总质量为m=80kg,以初速度v0=12m/s沿倾角为θ=37°的斜坡向上自由滑行,已知滑板与斜坡间动摩擦因数=0.25,假设斜坡足够长,斜坡可看成如图b所示的斜面,不计空气阻力(取g=10m/s2,sin37°=0.6,cos37°=0.8)。试求:

(1)滑雪者沿斜面上滑时加速度的大小;
(2)滑雪者沿斜面上滑的最大距离。
【答案】(1)a=8m/s2 (2)x=9m
【解析】(1)由牛顿第二定律得:mgsin37°+μmgcos37°=ma;
解得加速度大小为:a=gsin37°+μgcos37°=10×0.6+0.25×10×0.8=6+2=8m/s2;
(2)根据位移速度关系可得上滑的最大距离为:0v02=2ax
所以上滑的最大距离为: ![]()

【题目】图甲所示为某中学物理课外学习小组设计的测定当地重力加速度的实验装置,他们的主要操作如下:
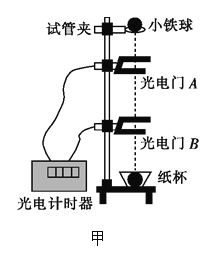
①安装实验器材,调节试管夹(小铁球)、光电门和纸杯在同一竖直线上。
②打开试管夹,由静止释放小铁球,用光电计时器记录小铁球在两个光电门间的运动时间t,并用刻度尺(图上未画出)测量出两个光电门之间的高度h,然后计算出小铁球通过两光电门间的平均速度v。
③固定光电门B的位置不变,改变光电门A的高度,重复②的操作。测出多组(h,t),并计算出对应的平均速度v。
④画出v-t图象。
请根据实验,回答如下问题:
(1)设小铁球到达光电门B时的速度为vB,当地的重力加速度为g,则小铁球通过两光电门间的平均速度v的表达式为_________。(用vB、g和t表示)
(2)实验测得的数据如表所示。
实验次数 | h/cm | t/s | v/(m·s-1) |
1 | 10.0 | 0.028 | 3.57 |
2 | 20.0 | 0.059 | 3.39 |
3 | 30.0 | 0.092 | 3.26 |
4 | 40.0 | 0.131 | 3.05 |
5 | 50.0 | 0.176 | 2.84 |
6 | 60.0 | 0.235 | 2.55 |
请在图乙所示坐标纸上画出v-t图象________。
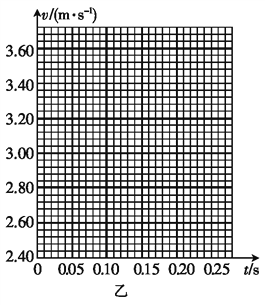
根据v-t图象,可以求得当地重力加速度g=___ m/s2。(结果保留3位有数数字)